题目内容
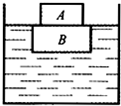 (2009?崇文区一模)一个竖直放置在水平桌面上的圆柱形容器,内装某种液体.将体积为V的金属块A挂在弹簧测力计下并浸没在该液体中(A与容器底未接触).金属块A静止时,弹簧测力计的示数为F.将木块B放入该液体中,静止后木块B露出液面的体积与其总体积之比为7:12,把金属块A放在木块B上面,木块B刚好没入液体中(如图所示).若已知金属块A的体积与木块B的体积之比为13:24,则金属块A的密度为
(2009?崇文区一模)一个竖直放置在水平桌面上的圆柱形容器,内装某种液体.将体积为V的金属块A挂在弹簧测力计下并浸没在该液体中(A与容器底未接触).金属块A静止时,弹簧测力计的示数为F.将木块B放入该液体中,静止后木块B露出液面的体积与其总体积之比为7:12,把金属块A放在木块B上面,木块B刚好没入液体中(如图所示).若已知金属块A的体积与木块B的体积之比为13:24,则金属块A的密度为| 14F |
| Vg |
| 14F |
| Vg |
分析:将木块B放入该液体中时漂浮,根据阿基米德原理和密度公式、重力公式得出等式得出B物体的密度和液体密度之间的关系;将木块B放入该液体中静止后木块仍漂浮,再根据阿基米德原理和密度公式、重力公式得出等式结合两者的体积关系求出物体A的密度和液体密度之间的关系,利用称重法表示出物体A浸没在该液体中时的浮力即可求出金属块A的密度.
解答:解:将木块B放入该液体中时漂浮,
由F浮=ρgV排和ρ=
、G=mg可得:
F浮=G木,即ρgVB(1-
)=ρBVBg
解得:ρB=
ρ,
把金属块A放在木块B上面时,A、B漂浮,则
F浮′=GA+GB,即ρgVB=ρAVAg+ρBVBg=ρAVAg+
ρVBg,
整理可得:ρVB=ρAVA+
ρVB,
∵VA:VB=13:24,
∴ρVB=ρA×
VB+
ρVB,
解得:ρ=
ρA,
∵金属块A挂在弹簧测力计下并浸没在该液体中静止时,弹簧测力计的示数为F,
∴根据称重法可得:
F浮A=GA-F,即ρgVA=
ρA×gVA=ρAVAg-F,
解得:ρA=
.
故答案为:
.
由F浮=ρgV排和ρ=
| m |
| V |
F浮=G木,即ρgVB(1-
| 7 |
| 12 |
解得:ρB=
| 5 |
| 12 |
把金属块A放在木块B上面时,A、B漂浮,则
F浮′=GA+GB,即ρgVB=ρAVAg+ρBVBg=ρAVAg+
| 5 |
| 12 |
整理可得:ρVB=ρAVA+
| 5 |
| 12 |
∵VA:VB=13:24,
∴ρVB=ρA×
| 13 |
| 24 |
| 5 |
| 12 |
解得:ρ=
| 13 |
| 14 |
∵金属块A挂在弹簧测力计下并浸没在该液体中静止时,弹簧测力计的示数为F,
∴根据称重法可得:
F浮A=GA-F,即ρgVA=
| 13 |
| 14 |
解得:ρA=
| 14F |
| Vg |
故答案为:
| 14F |
| Vg |
点评:本题考查了密度的计算,涉及到阿基米德原理、物体浮沉条件和重力公式,根据浮沉条件得出AB密度和液体密度之间的关系是关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 (2009?崇文区一模)如图所示,电源电压为12V且保持不变,小灯泡L 的规格为“6V 3W”,滑动变阻器的最大阻值为12Ω,电流表的量程为0~3A,当开关S1、S2都断开时,小灯泡L恰能正常发光,则下列说法正确的是( )
(2009?崇文区一模)如图所示,电源电压为12V且保持不变,小灯泡L 的规格为“6V 3W”,滑动变阻器的最大阻值为12Ω,电流表的量程为0~3A,当开关S1、S2都断开时,小灯泡L恰能正常发光,则下列说法正确的是( )