题目内容
 如图所示,在容器底部固定一轻质弹簧,弹簧上端连有一长方体木块A,容器侧面的底部有一由阀门B控制的出水口.最初当容器中水深为20cm时,木块A有
如图所示,在容器底部固定一轻质弹簧,弹簧上端连有一长方体木块A,容器侧面的底部有一由阀门B控制的出水口.最初当容器中水深为20cm时,木块A有| 3 |
| 5 |
(1)现向容器内缓慢加水,直至木块A刚好完全浸没水中,此时弹簧对木块A的作用力为F1,然后打开阀门B缓慢放水,直至木块A刚好完全离开水面,此时弹簧对木块A的作用力为F2,求
| F1 |
| F2 |
(2)如果在最初状态的情况下打开阀门B,试求最先冲出出水口的水流速度v=?
分析:(1)最初当容器中水深为20cm时,木块A有
的体积浸在水中,弹簧恰好处于自然伸长状态,没有发生形变,木块处于漂浮状态,根据F浮=ρ水v排g=G=ρ木vg求木块的密度;
向容器内缓慢加水,当木块A刚好完全浸没水中时,弹簧对木块A的作用力F1=F浮-G;
打开阀门B缓慢放水,直至木块A刚好完全离开水面,此时浮力为0,弹簧对木块A的作用力F2和木块的重力是一对平衡力,两者相等,F2=G,据此求F1和F2的比值;
(2)根据机械能守恒,处于h高的水到容器底,重力势能转化动能,mgh=
mv2求最先冲出出水口的水流速度v.
| 3 |
| 5 |
向容器内缓慢加水,当木块A刚好完全浸没水中时,弹簧对木块A的作用力F1=F浮-G;
打开阀门B缓慢放水,直至木块A刚好完全离开水面,此时浮力为0,弹簧对木块A的作用力F2和木块的重力是一对平衡力,两者相等,F2=G,据此求F1和F2的比值;
(2)根据机械能守恒,处于h高的水到容器底,重力势能转化动能,mgh=
| 1 |
| 2 |
解答:解:(1)由题知,起初木块漂浮在水面上,
F浮=ρ水v排g=ρ水
vg=G=ρ木vg,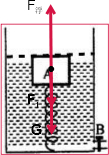
∴ρ木=
ρ水,
当木块A刚好完全浸没水中时,如图,弹簧对木块A的作用力:
F1=F浮-G=ρ水gV-ρ木gV,
由于物体A刚好离开水面,所以不再受浮力作用,则有:
F2=G=ρ木gV,
=
=
=
=
;
(2)在最初状态的情况下,水深h=20cm=0.2m,
∵mgh=
mv2,
∴最先冲出出水口的水流速度:
v=
=
=2m/s.
答:F1和F2的比值为2:3;
(2)最先冲出出水口的水流速度为2m/s.
F浮=ρ水v排g=ρ水
| 3 |
| 5 |

∴ρ木=
| 3 |
| 5 |
当木块A刚好完全浸没水中时,如图,弹簧对木块A的作用力:
F1=F浮-G=ρ水gV-ρ木gV,
由于物体A刚好离开水面,所以不再受浮力作用,则有:
F2=G=ρ木gV,
| F1 |
| F2 |
| ρ水gV -ρ木Vg |
| ρ木Vg |
| ρ水- ρ木 |
| ρ木 |
ρ水-
| ||
|
| 2 |
| 3 |
(2)在最初状态的情况下,水深h=20cm=0.2m,
∵mgh=
| 1 |
| 2 |
∴最先冲出出水口的水流速度:
v=
| 2gh |
| 2×10N/kg×0.2m |
答:F1和F2的比值为2:3;
(2)最先冲出出水口的水流速度为2m/s.
点评:本题考查了阿基米德原理、物体的漂浮条件、力的合成、动能和重力势能的相互转化与守恒,知识点多、综合性强,要求灵活运用所学公式.

练习册系列答案
相关题目
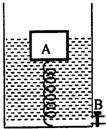 如图所示,在容器底部固定一轻质弹簧,弹簧上方连有长方体木块A,容器侧面的底部有一个由阀门B控制的出水口,当容器中水深为20cm时,木块A有
如图所示,在容器底部固定一轻质弹簧,弹簧上方连有长方体木块A,容器侧面的底部有一个由阀门B控制的出水口,当容器中水深为20cm时,木块A有 如图所示,在容器底部固定一轻质弹簧,弹簧上方连有长方体木块A,容器侧面的底部有一个由阀门B控制的出水口,当容器中水深为20cm时,木块A有一半的体积浸在水中,此时弹簧恰好处于自然状态,没有发生形变.(不计弹簧受到的浮力,g取10N/kg.)
如图所示,在容器底部固定一轻质弹簧,弹簧上方连有长方体木块A,容器侧面的底部有一个由阀门B控制的出水口,当容器中水深为20cm时,木块A有一半的体积浸在水中,此时弹簧恰好处于自然状态,没有发生形变.(不计弹簧受到的浮力,g取10N/kg.) (2013?荆门)如图所示,在容器底部固定一轻质弹簧,弹簧上方连有正方体木块A,容器侧面的底部有一个由阀门B控制的出水口,当容器中水深为20cm时,木块A有
(2013?荆门)如图所示,在容器底部固定一轻质弹簧,弹簧上方连有正方体木块A,容器侧面的底部有一个由阀门B控制的出水口,当容器中水深为20cm时,木块A有 如图所示,在容器底部固定一轻质弹簧,弹簧上方连有长方体木块A,容器侧面的底 部有一个由阀门B控制的出水口,当容器中水深为20cm时,木块A有2/5的体积浸在水中,此时弹簧恰好处于自然状态,没有发生形变.(不计弹簧受到的浮力,g取10N/kg.)
如图所示,在容器底部固定一轻质弹簧,弹簧上方连有长方体木块A,容器侧面的底 部有一个由阀门B控制的出水口,当容器中水深为20cm时,木块A有2/5的体积浸在水中,此时弹簧恰好处于自然状态,没有发生形变.(不计弹簧受到的浮力,g取10N/kg.)