题目内容
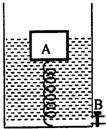
 如图所示,在容器底部固定一轻质弹簧,弹簧上方连有长方体木块A,容器侧面的底部有一个由阀门B控制的出水口,当容器中水深为20cm时,木块A有一半的体积浸在水中,此时弹簧恰好处于自然状态,没有发生形变.(不计弹簧受到的浮力,g取10N/kg.)
如图所示,在容器底部固定一轻质弹簧,弹簧上方连有长方体木块A,容器侧面的底部有一个由阀门B控制的出水口,当容器中水深为20cm时,木块A有一半的体积浸在水中,此时弹簧恰好处于自然状态,没有发生形变.(不计弹簧受到的浮力,g取10N/kg.)(1)求此时容器底部受到的水的压强;
(2)求木块A的密度;
(3)向容器内缓慢加水,直至木块A刚好完全浸没水中,立即停止加水,此时弹簧对木块A的作用力为F1,在原图上画出此时水面的大致位置;
(4)打开阀门B缓慢放水,直至木块A刚好完全离开水面时,立即关闭阀门B,此时弹簧对木块A的作用力为F2,求F1、F2之比.
分析:(1)已知容器中水的深度,根据p=ρgh求出容器底部受到的水的压强;
(2)木块漂浮时受到的浮力和自身的重力相等,根据G=mg=ρVg和F浮=ρ液gV排得出表达式,即可求出木块的密度;
(3)弹簧对木块有向下的拉力,所以向容器中加水时,随着木块浸入水中体积的增大,所受浮力增大,直到木块完全浸没浮力不再变化.
(4)木块完全浸没时,弹簧对木块有向下的拉力F1;木块离开水面时,弹簧对木块有向上的支持力F2,分别计算F1、F2的大小,就能得到两者之比.
(2)木块漂浮时受到的浮力和自身的重力相等,根据G=mg=ρVg和F浮=ρ液gV排得出表达式,即可求出木块的密度;
(3)弹簧对木块有向下的拉力,所以向容器中加水时,随着木块浸入水中体积的增大,所受浮力增大,直到木块完全浸没浮力不再变化.
(4)木块完全浸没时,弹簧对木块有向下的拉力F1;木块离开水面时,弹簧对木块有向上的支持力F2,分别计算F1、F2的大小,就能得到两者之比.
解答:解:
(1)容器底部受到的水的压强:
p=ρ水gh=1.0×103kg/m3×10N/kg×0.2m=2000Pa;
(2)因木块漂浮,
所以G=F浮,即ρ木gV=ρ水g×
V,
解得:ρ木=
ρ水=0.5×103kg/m3;
(3)木块完全浸没时,受到的浮力最大,此时弹簧略向上伸长,所以画水面位置时,应在木块位置略高一些,如下图所示:
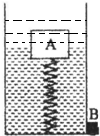
(4)木块完全浸没时,弹簧对木块的作用力:
F1=F浮-G=ρ水gV-ρ木gV=0.5ρ水gV,
木块离开水面后,弹簧对木块的作用力:
F2=G=ρ木gV=0.5ρ水gV,
所以F1:F2=0.5ρ水gV:0.5ρ水gV=1:1.
答:(1)此时容器底部受到的水的压强为2000Pa;
(2)木块A的密度为0.5×103kg/m3;
(3)如上图所示;
(4)F1、F2之比为1:1.
(1)容器底部受到的水的压强:
p=ρ水gh=1.0×103kg/m3×10N/kg×0.2m=2000Pa;
(2)因木块漂浮,
所以G=F浮,即ρ木gV=ρ水g×
| 1 |
| 2 |
解得:ρ木=
| 1 |
| 2 |
(3)木块完全浸没时,受到的浮力最大,此时弹簧略向上伸长,所以画水面位置时,应在木块位置略高一些,如下图所示:

(4)木块完全浸没时,弹簧对木块的作用力:
F1=F浮-G=ρ水gV-ρ木gV=0.5ρ水gV,
木块离开水面后,弹簧对木块的作用力:
F2=G=ρ木gV=0.5ρ水gV,
所以F1:F2=0.5ρ水gV:0.5ρ水gV=1:1.
答:(1)此时容器底部受到的水的压强为2000Pa;
(2)木块A的密度为0.5×103kg/m3;
(3)如上图所示;
(4)F1、F2之比为1:1.
点评:本题考查了学生对液体压强公式、密度公式、物体浮沉条件的理解与掌握,明确弹簧因受力不同形变不同和木块浸没时弹簧对木块有向下的拉力、木块离开水后弹簧对木块有向上的支持力是正确解答的关键.

练习册系列答案
相关题目
 如图所示,在容器底部固定一轻质弹簧,弹簧上方连有长方体木块A,容器侧面的底部有一个由阀门B控制的出水口,当容器中水深为20cm时,木块A有
如图所示,在容器底部固定一轻质弹簧,弹簧上方连有长方体木块A,容器侧面的底部有一个由阀门B控制的出水口,当容器中水深为20cm时,木块A有 如图所示,在容器底部固定一轻质弹簧,弹簧上端连有一长方体木块A,容器侧面的底部有一由阀门B控制的出水口.最初当容器中水深为20cm时,木块A有
如图所示,在容器底部固定一轻质弹簧,弹簧上端连有一长方体木块A,容器侧面的底部有一由阀门B控制的出水口.最初当容器中水深为20cm时,木块A有 (2013?荆门)如图所示,在容器底部固定一轻质弹簧,弹簧上方连有正方体木块A,容器侧面的底部有一个由阀门B控制的出水口,当容器中水深为20cm时,木块A有
(2013?荆门)如图所示,在容器底部固定一轻质弹簧,弹簧上方连有正方体木块A,容器侧面的底部有一个由阀门B控制的出水口,当容器中水深为20cm时,木块A有 如图所示,在容器底部固定一轻质弹簧,弹簧上方连有长方体木块A,容器侧面的底 部有一个由阀门B控制的出水口,当容器中水深为20cm时,木块A有2/5的体积浸在水中,此时弹簧恰好处于自然状态,没有发生形变.(不计弹簧受到的浮力,g取10N/kg.)
如图所示,在容器底部固定一轻质弹簧,弹簧上方连有长方体木块A,容器侧面的底 部有一个由阀门B控制的出水口,当容器中水深为20cm时,木块A有2/5的体积浸在水中,此时弹簧恰好处于自然状态,没有发生形变.(不计弹簧受到的浮力,g取10N/kg.)