题目内容
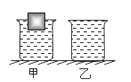
【题目】如图所示,一实心正方体铝块浸没在密度为0.9×103kg/m3的油中,其质量为2.7kg,上表面与液面相平行,上、下表面的深度分别为h1和h2 , 且2h1=h2=20cm,求:
①铝块上表面处的液体压强;
②若使铝块在图示位置处于静止状态,还应使其在竖直方向受到一个多大的力;
③若图中正方体是由密度为3.6×103kg/m3的合金制成,且处于悬浮状态,则该正方体空心部分体积是多少?
【答案】解:①铝块上表面所处的深度:
h1=10cm=0.1m,
铝块上表面处的液体压强:
p1=ρgh1=0.9×103kg/m3×10N/kg×0.1m=900Pa;
②正方体的边长:
L=h2﹣h1=0.2m﹣0.1m=0.1m,
正方体铝块的体积:
V=L3=(0.1m)3=10﹣3m3 ,
正方体铝块浸没时受到的浮力:
F浮=ρgV排=ρgV=0.9×103kg/m3×10N/kg×10﹣3m3=9N,
因铝块静止时处于平衡状态,受到的力为平衡力,
所以,施加的力:
F=G﹣F浮=mg﹣F浮=2.7kg×10N/kg﹣9N=18N,
即施加竖直向上18N的力;
③合金处于悬浮状态时受到的浮力和自身的重力相等,
则合金的质量:
m′= ![]() =
= ![]() =
= ![]() =0.9kg,
=0.9kg,
由ρ= ![]() 可得,正方体中合金的体积:
可得,正方体中合金的体积:
V′= ![]() =
= ![]() =2.5×10﹣4m3 ,
=2.5×10﹣4m3 ,
空心部分的体积:
V空=V﹣V′=10﹣3m3﹣2.5×10﹣4m3=7.5×10﹣4m3 .
答:①铝块上表面处的液体压强为900Pa;②若使铝块在图示位置处于静止状态,还应使其在竖直方向受到一个18N的力;③若图中正方体是由密度为3.6×103kg/m3的合金制成,且处于悬浮状态,则该正方体空心部分体积是7.5×10﹣4m3 .
【解析】①由题意可知铝块上表面所处的深度,根据p=ρgh求出受到的液态压强;②正方体上下表面所处深度的差值即为其边长,根据V=L3求出正方体的体积,根据阿基米德原理求出受到的浮力,铝块静止时处于平衡状态,受到的力为平衡力,根据力的平衡求出竖直方向施加的力;③合金处于悬浮状态时受到的浮力和自身的重力相等,根据G=mg求出合金的质量,根据ρ= ![]() 求出正方体中合金的体积,正方体的体积减去合金的体积即为空心部分的体积.本题考查了液体压强公式和阿基米德原理、密度公式、重力公式的应用以及平衡条件的应用,利用好漂浮或悬浮时受到的浮力等于自身的重力是关键.
求出正方体中合金的体积,正方体的体积减去合金的体积即为空心部分的体积.本题考查了液体压强公式和阿基米德原理、密度公式、重力公式的应用以及平衡条件的应用,利用好漂浮或悬浮时受到的浮力等于自身的重力是关键.
【考点精析】关于本题考查的液体的压强的计算和浮力大小的计算,需要了解液体内部压强的公式:p=ρgh ρ指密度,单位kg/m3,g=9.8N/kg, h指深度,单位:m,压强单位(Pa) 注意:h 指液体的深度,即某点到液面的距离;浮力的公式为:F浮= G排 =ρ液gv排才能得出正确答案.

【题目】电热加湿器靠电流的热效应工作.某种家用电热加湿器相关参数、外形、电路简化图如图所示.电热器的电热丝浸没在加热仓的水中产生热量,使加热中的水沸腾变成水蒸气喷出,增加环境湿度.当加热仓中的水减少到一定程度时,自动阀门智能打开,水由储水箱进入到加热仓中.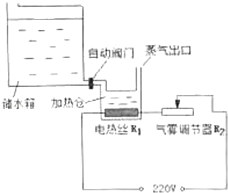
工作电压 | 220V |
工作频率 | 50Hz |
最大运行功率 | 40W |
储水箱容量 | 2.4L |
尺寸 | 高315mm,底部直径168mm |
满水工作时间 | 高气雾量10h,低气雾量24h |
①当气雾调节器R2的滑片移到最左边时,加湿器以最大运行功率工作,求电热丝R1的电阻值.
②如果加热仓内冷水的温度为20℃,用最大运行功率工作,经过5min36s,水沸腾产生蒸气,求加热仓中水的体积.[c水=4.2×103J/(kg℃).ρ水=1×103kg/m3 , 电热丝R1产生的热量全部被水吸收.环境为标准大气压].
③当滑片移到最右端时,气雾调节器R2的阻值为605Ω,加湿器以最低气雾量工作,求此时电热丝R1的电功率是多少瓦?24小时R1消耗多少度电?(计算结果保留一位小数)