题目内容
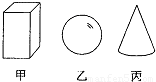
 如图所示,水平桌面上放一底面积为100cm2的柱形容器,容器内盛有某种液体,滑轮组左端挂一重物,并浸没在液体中,当用滑轮组提升浸没在液体中的物体时,竖直向下拉动滑轮的力为11.8N,液体对容器底的压强为2000Pa;当将物体上提到
如图所示,水平桌面上放一底面积为100cm2的柱形容器,容器内盛有某种液体,滑轮组左端挂一重物,并浸没在液体中,当用滑轮组提升浸没在液体中的物体时,竖直向下拉动滑轮的力为11.8N,液体对容器底的压强为2000Pa;当将物体上提到 体积露出液面时,竖直向下拉动滑轮的力为13.4N;已知物体的密度为5.0×103kg/m3,每个滑轮的重力为1N,忽略绳重、轮与轴之间的摩擦,取g=10N/kg.求:
体积露出液面时,竖直向下拉动滑轮的力为13.4N;已知物体的密度为5.0×103kg/m3,每个滑轮的重力为1N,忽略绳重、轮与轴之间的摩擦,取g=10N/kg.求:
(1)物体的重力;
(2)液体的密度;
(3)当物体上提到 体积露出液面时液体对容器底的压强.
体积露出液面时液体对容器底的压强.
解:(1)由图示滑轮组可知,滑轮组承重绳子的股数n=2,
设绳子的拉力为T,2T=F+G动滑轮,
绳子拉力T1= =
= =6.4N,
=6.4N,
T2= =
= =7.2N,
=7.2N,
重物静止,处于平衡状态,则G=F浮+T,
∵ρ=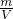 ,∴物体重力G=mg=ρgV,
,∴物体重力G=mg=ρgV,
物体在液体中受到的浮力F浮=ρ液gV排,
设物体的体积为V,物体密度为ρ,由G=F浮+T得:
ρgV=ρ液gV+T1,ρgV=ρ液g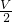 +T2,
+T2,
5.0×103kg/m3×10N/kg×V=ρ液×10N/kg×V+6.4N ①,
5.0×103kg/m3×10N/kg×V=ρ液×10N/kg×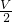 +7.2N ②,
+7.2N ②,
由2②-①解得:V=1.6×10-4m3,
将V代入①解得:ρ液=1×103kg/m3;
物体的重力G=ρgV=5.0×103kg/m3×10N/kg×1.6×10-4m3=8N;
(2)由(1)可知,液体的密度为ρ液=1×103kg/m3;
(3)当物体上提到 体积露出液面时,液体深度的变化量:
体积露出液面时,液体深度的变化量:
△h=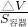 =
= =
= =8×10-3m,
=8×10-3m,
液体压强的变化量△p=ρg△h=1×103kg/m3×10N/kg×8×10-3m=80Pa,
物体提出液面,物体排开液体的体积变小,液面下降,
当物体上提到 体积露出液面时液体对容器底的压强:
体积露出液面时液体对容器底的压强:
p′=p-△p=2000Pa-80Pa=1920Pa;
答:(1)物体的重力为8N;
(2)液体的密度为1×103kg/m3;
(3)当物体上提到 体积露出液面时液体对容器底的压强为1920Pa.
体积露出液面时液体对容器底的压强为1920Pa.
分析:(1)(2)由图示滑轮组可知,滑轮组承重绳子的股数n=2,由滑轮组公式可以求出绳子的拉力;对物体受力分析,由平衡条件列方程,应用密度公式的变形公式、浮力公式可以求出物体的体积与液体的密度,然后由此物体的重力;
(3)求出物体上升到一半体积露出液面时液体深度的变化量,然后由液体压强公式求出液体对容器底的压强.
点评:本题难度较大,是一道难题,应用滑轮组公式、浮力公式、密度公式的变形公式、液体压强公式进行分析答题,解题时注意单位换算.
设绳子的拉力为T,2T=F+G动滑轮,
绳子拉力T1=
 =
= =6.4N,
=6.4N,T2=
 =
= =7.2N,
=7.2N,重物静止,处于平衡状态,则G=F浮+T,
∵ρ=
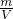 ,∴物体重力G=mg=ρgV,
,∴物体重力G=mg=ρgV,物体在液体中受到的浮力F浮=ρ液gV排,
设物体的体积为V,物体密度为ρ,由G=F浮+T得:
ρgV=ρ液gV+T1,ρgV=ρ液g
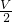 +T2,
+T2,5.0×103kg/m3×10N/kg×V=ρ液×10N/kg×V+6.4N ①,
5.0×103kg/m3×10N/kg×V=ρ液×10N/kg×
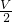 +7.2N ②,
+7.2N ②,由2②-①解得:V=1.6×10-4m3,
将V代入①解得:ρ液=1×103kg/m3;
物体的重力G=ρgV=5.0×103kg/m3×10N/kg×1.6×10-4m3=8N;
(2)由(1)可知,液体的密度为ρ液=1×103kg/m3;
(3)当物体上提到
 体积露出液面时,液体深度的变化量:
体积露出液面时,液体深度的变化量:△h=
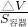 =
= =
= =8×10-3m,
=8×10-3m,液体压强的变化量△p=ρg△h=1×103kg/m3×10N/kg×8×10-3m=80Pa,
物体提出液面,物体排开液体的体积变小,液面下降,
当物体上提到
 体积露出液面时液体对容器底的压强:
体积露出液面时液体对容器底的压强:p′=p-△p=2000Pa-80Pa=1920Pa;
答:(1)物体的重力为8N;
(2)液体的密度为1×103kg/m3;
(3)当物体上提到
 体积露出液面时液体对容器底的压强为1920Pa.
体积露出液面时液体对容器底的压强为1920Pa.分析:(1)(2)由图示滑轮组可知,滑轮组承重绳子的股数n=2,由滑轮组公式可以求出绳子的拉力;对物体受力分析,由平衡条件列方程,应用密度公式的变形公式、浮力公式可以求出物体的体积与液体的密度,然后由此物体的重力;
(3)求出物体上升到一半体积露出液面时液体深度的变化量,然后由液体压强公式求出液体对容器底的压强.
点评:本题难度较大,是一道难题,应用滑轮组公式、浮力公式、密度公式的变形公式、液体压强公式进行分析答题,解题时注意单位换算.

练习册系列答案
相关题目
 (2010?天津模拟)用相同材料,相同质量的物质做成实心的长方体,球体和圆锥体如图所示放在水平桌面上,若三个物体对桌面的压力和压强分别为F甲、F乙、F丙及p甲、p乙、p丙,则下述关系正确的是
(2010?天津模拟)用相同材料,相同质量的物质做成实心的长方体,球体和圆锥体如图所示放在水平桌面上,若三个物体对桌面的压力和压强分别为F甲、F乙、F丙及p甲、p乙、p丙,则下述关系正确的是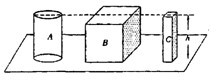 高度相同的实心圆柱体A、正方体B和长方体C铁块如图所示放在水平桌面上,已知正方体铁块最重,长方体铁块底面积最小,针对“这三个铁块对桌面的压强哪一块最大”的问题,同学们提出了以下三个猜想:
高度相同的实心圆柱体A、正方体B和长方体C铁块如图所示放在水平桌面上,已知正方体铁块最重,长方体铁块底面积最小,针对“这三个铁块对桌面的压强哪一块最大”的问题,同学们提出了以下三个猜想: 洋洋家有一个如图所示放在水平桌面上的“海宝”的摆件.已知“海宝”是实心的,洋洋很想知道它是什么材料制成的,于是设法测得了它的质量是2.56kg,体积是3×10-4m3.
洋洋家有一个如图所示放在水平桌面上的“海宝”的摆件.已知“海宝”是实心的,洋洋很想知道它是什么材料制成的,于是设法测得了它的质量是2.56kg,体积是3×10-4m3.