题目内容
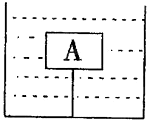 木块A的体积为500cm3,质量为300g,用细线拉着浸没于盛水的圆柱形容器中,容器的底面积为100cm2,容器内水面高度为30cm,如图所示,求:(ρ水=1.0×103kg/m3,g取10N/kg)
木块A的体积为500cm3,质量为300g,用细线拉着浸没于盛水的圆柱形容器中,容器的底面积为100cm2,容器内水面高度为30cm,如图所示,求:(ρ水=1.0×103kg/m3,g取10N/kg)(1)物体受到的浮力;
(2)水对容器底的压强;
(3)绳子的拉力T;
(4)若剪断绳子后,木块静止时,水对容器底的压强.
分析:(1)已知木块浸没于盛水的圆柱形容器中,根据木块体积利用阿基米德原理可求所受浮力;
(2)已知水的深度可求压强;
(3)根据二力平衡可求可求绳子拉力;
(4)绳子剪断后,木块漂浮,浮力等于重力,算出排开水的体积,根据总体积减去排开水的体积就是减小的水的体积,从而算出减小的水深度,进一步算出水的深度,求出水对容器底部的压强.
(2)已知水的深度可求压强;
(3)根据二力平衡可求可求绳子拉力;
(4)绳子剪断后,木块漂浮,浮力等于重力,算出排开水的体积,根据总体积减去排开水的体积就是减小的水的体积,从而算出减小的水深度,进一步算出水的深度,求出水对容器底部的压强.
解答:解:(1)∵木块浸没于盛水的圆柱形容器中,则V排=V木=500cm3=5×10-4m3,
∴根据阿基米德原理木块受到的浮力F浮=ρ水gV排=1.0×103kg/m3×10N/kg×5×10-4m3=5N.
(2)水对容器底的压强p=ρ水gh=1.0×103kg/m3×10N/kg×0.3m=3000Pa.
(3)∵F浮=G+T,∴T=F浮-G=5N-mg=5N-0.3kg×10N/kg=2N.
(4)若剪断绳子后,木块漂浮,F浮′=G=mg=ρgV排,
∴V排=
=
=3×10-4m3=300cm3;
V减=V-V排=500-300cm3=200cm3
∴h减=
=
=2cm=0.02m.
木块静止时,水对容器底的压强p1=ρ水g(h-h减)=1.0×103kg/m3×10N/kg×(0.3m-0.02m)=2800Pa.
答:(1)物体受到的浮力为5N;
(2)水对容器底的压强为3000Pa;
(3)绳子的拉力T为2N;
(4)若剪断绳子后,木块静止时,水对容器底的压强是2800Pa.
∴根据阿基米德原理木块受到的浮力F浮=ρ水gV排=1.0×103kg/m3×10N/kg×5×10-4m3=5N.
(2)水对容器底的压强p=ρ水gh=1.0×103kg/m3×10N/kg×0.3m=3000Pa.
(3)∵F浮=G+T,∴T=F浮-G=5N-mg=5N-0.3kg×10N/kg=2N.
(4)若剪断绳子后,木块漂浮,F浮′=G=mg=ρgV排,
∴V排=
| m |
| ρ水 |
| 0.3kg |
| 1×103kg/m3 |
V减=V-V排=500-300cm3=200cm3
∴h减=
| V减 |
| S |
| 200cm3 |
| 100cm2 |
木块静止时,水对容器底的压强p1=ρ水g(h-h减)=1.0×103kg/m3×10N/kg×(0.3m-0.02m)=2800Pa.
答:(1)物体受到的浮力为5N;
(2)水对容器底的压强为3000Pa;
(3)绳子的拉力T为2N;
(4)若剪断绳子后,木块静止时,水对容器底的压强是2800Pa.
点评:本题考查液体压强和浮力的计算,利用阿基米德原理和二力平衡条件的分析解答.

练习册系列答案
相关题目
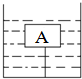 木块A的体积为500cm3,质量为300g,用细线拉着浸没于盛水的圆柱形容器中,容器的底面积为100cm2,容器内水面高度为30cm,如图所示,求:
木块A的体积为500cm3,质量为300g,用细线拉着浸没于盛水的圆柱形容器中,容器的底面积为100cm2,容器内水面高度为30cm,如图所示,求: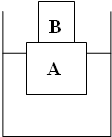 (2000?北京)木块A漂浮在容器中的水面上,它的上面放有一块石块B,如图所示,此时木块A排开水的体积为V1.若将石块B从木块A上取下,放入水中,静止时,木块A和石块B排开水的总体积为V2.已知V1-V2=2分米3,木块A的体积为4分米3,石块B的密度为3×103千克/米3,g=10牛/千克.则容器底对石块B的支持力为( )
(2000?北京)木块A漂浮在容器中的水面上,它的上面放有一块石块B,如图所示,此时木块A排开水的体积为V1.若将石块B从木块A上取下,放入水中,静止时,木块A和石块B排开水的总体积为V2.已知V1-V2=2分米3,木块A的体积为4分米3,石块B的密度为3×103千克/米3,g=10牛/千克.则容器底对石块B的支持力为( )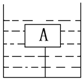 (2012?峨眉山市二模)木块A的体积为500cm3,质量为300g,用细线拉着浸没于盛水的圆柱形容器中,容器的底面积为100cm2,容器内水面高度为30cm.如图所示,求:
(2012?峨眉山市二模)木块A的体积为500cm3,质量为300g,用细线拉着浸没于盛水的圆柱形容器中,容器的底面积为100cm2,容器内水面高度为30cm.如图所示,求: (2008?房山区一模)如图所示,在木块A上放一金属块B后,木块A恰好没入水中,此时水对容器底的压强为P1.将金属块B从木块A上取下,放入水中并浸没,静止时容器底对金属块B的支持力为20N,此时水对容器底的压强为P2.已知木块A的体积为7.5×10-3m3,金属块B的密度为3×103kg/m3,取g=10N/kg.则( )
(2008?房山区一模)如图所示,在木块A上放一金属块B后,木块A恰好没入水中,此时水对容器底的压强为P1.将金属块B从木块A上取下,放入水中并浸没,静止时容器底对金属块B的支持力为20N,此时水对容器底的压强为P2.已知木块A的体积为7.5×10-3m3,金属块B的密度为3×103kg/m3,取g=10N/kg.则( )