题目内容
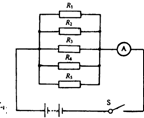 如图所示,将R1、R2、R3、R4、R5五只阻值不等的电阻并联后接在电源电压为6伏的电路中,若电阻R1的阻值为50欧,R5为10欧,且R1>R2>R3>R4>R5.当电键S闭合后,可判断电流表的示数范围是
如图所示,将R1、R2、R3、R4、R5五只阻值不等的电阻并联后接在电源电压为6伏的电路中,若电阻R1的阻值为50欧,R5为10欧,且R1>R2>R3>R4>R5.当电键S闭合后,可判断电流表的示数范围是1.08A<I<2.52A
1.08A<I<2.52A
.分析:从图可知,电阻R1、R2、R3、R4、R5并联,知道电阻R1和R5的阻值,当电阻R2、R3、R4三个的阻值最大时,则整个并联电路的电阻就最大,利用并联电路电阻的特点计算出此时电路中的总电阻,再利用公式I=
计算出电路中的最小电流; 当电阻R2、R3、R4三个的阻值最小时,则整个并联电路的电阻就最小,利用并联电路电阻的特点计算出此时电路中的总电阻,再利用公式I=
计算出电路中的最大电流; 即可可判断电流表的示数范围.
| U |
| R |
| U |
| R |
解答:解:
从图可知,电阻R1、R2、R3、R4、R5并联,知道电阻R1和R5的阻值,
当电阻R2、R3、R4三个的阻值最大时,则整个并联电路的电阻就最大,
当让它们尽可能取最大值时,它们只可能接近电阻R1,但必须小于R1,
取R2=R3=R4=50Ω,
而R1=50Ω,R5=10Ω,
∴此时电路中的总电阻为:
=
+
+
+
+
=
+
+
+
+
=
,
解得:R大≈5.56Ω,
而U=6V,
∴此时电路中的最小电流为:I小=
=
≈1.08A;
当电阻R2、R3、R4三个的阻值最小时,则整个并联电路的电阻就最小,
当让它们尽可能取最小值时,它们只可能接近电阻R5,但必须大于R5,
取R2=R3=R4=10Ω,
而R1=50Ω,R5=10Ω,
∴此时电路中的总电阻为:
=
+
+
+
+
=
+
+
+
+
=
,
解得:R小≈2.38Ω,
而U=6V,
∴此时电路中的最大电流为:I大=
=
≈2.52A;
事实上计算出的I小和I大都是这一电路中可以接近但不能达到的数值,
故电流表的示数范围为:1.08A<I<2.52A.
故答案为:1.08A<I<2.52A.
从图可知,电阻R1、R2、R3、R4、R5并联,知道电阻R1和R5的阻值,
当电阻R2、R3、R4三个的阻值最大时,则整个并联电路的电阻就最大,
当让它们尽可能取最大值时,它们只可能接近电阻R1,但必须小于R1,
取R2=R3=R4=50Ω,
而R1=50Ω,R5=10Ω,
∴此时电路中的总电阻为:
| 1 |
| R大 |
| 1 |
| R1 |
| 1 |
| R2 |
| 1 |
| R3 |
| 1 |
| R4 |
| 1 |
| R5 |
| 1 |
| 50Ω |
| 1 |
| 50Ω |
| 1 |
| 50Ω |
| 1 |
| 50Ω |
| 1 |
| 10Ω |
| 9 |
| 50Ω |
解得:R大≈5.56Ω,
而U=6V,
∴此时电路中的最小电流为:I小=
| U |
| R大 |
| 6V |
| 5.56Ω |
当电阻R2、R3、R4三个的阻值最小时,则整个并联电路的电阻就最小,
当让它们尽可能取最小值时,它们只可能接近电阻R5,但必须大于R5,
取R2=R3=R4=10Ω,
而R1=50Ω,R5=10Ω,
∴此时电路中的总电阻为:
| 1 |
| R小 |
| 1 |
| R1 |
| 1 |
| R2 |
| 1 |
| R3 |
| 1 |
| R4 |
| 1 |
| R5 |
| 1 |
| 50Ω |
| 1 |
| 10Ω |
| 1 |
| 10Ω |
| 1 |
| 10Ω |
| 1 |
| 10Ω |
| 21 |
| 50Ω |
解得:R小≈2.38Ω,
而U=6V,
∴此时电路中的最大电流为:I大=
| U |
| R小 |
| 6V |
| 2.38Ω |
事实上计算出的I小和I大都是这一电路中可以接近但不能达到的数值,
故电流表的示数范围为:1.08A<I<2.52A.
故答案为:1.08A<I<2.52A.
点评:本题考查了并联电路电阻的特点,以及欧姆定律的应用,关键是在解题过程中对于电阻R2、R3、R4三个的阻值的确定.

练习册系列答案
相关题目
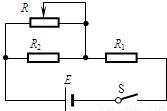
 (2008?昌平区二模)如图所示的电路中,R为滑动变阻器,R1、R2为定值电阻,且R1>R2,E为电压恒定的电源,当滑动变阻器的滑片滑动时,通过R、R1、R2的电流将发生变化,电流变化值分别为△I、△I1、△I2表示,则( )
(2008?昌平区二模)如图所示的电路中,R为滑动变阻器,R1、R2为定值电阻,且R1>R2,E为电压恒定的电源,当滑动变阻器的滑片滑动时,通过R、R1、R2的电流将发生变化,电流变化值分别为△I、△I1、△I2表示,则( ) 某研究性学习小组需要对两只定值电阻R1、R2和一只滑动变阻器R的阻值进行测定.如图所示,将这些元件连接成电路,电源电压不变.闭合开关S1,断开S2,将滑动变阻器的阻值调到最大时,电流表的示数为0.2A,电压表的读数为2V,若将开关S1、S2都闭合,将滑动变阻器的滑片调到阻值为零处,电压表读数为6V,电流表的示数为0.9A.求:
某研究性学习小组需要对两只定值电阻R1、R2和一只滑动变阻器R的阻值进行测定.如图所示,将这些元件连接成电路,电源电压不变.闭合开关S1,断开S2,将滑动变阻器的阻值调到最大时,电流表的示数为0.2A,电压表的读数为2V,若将开关S1、S2都闭合,将滑动变阻器的滑片调到阻值为零处,电压表读数为6V,电流表的示数为0.9A.求: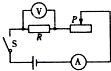 在探究“电流与电阻的关系”实验中,电路如图所示,其中定值R有R1=5Ω、R2=10Ω、R3=15Ω三种规格备用.
在探究“电流与电阻的关系”实验中,电路如图所示,其中定值R有R1=5Ω、R2=10Ω、R3=15Ω三种规格备用.