题目内容
一种液体的密度随深度而增大，它的变化规律是ρ=ρ0+kh，式中ρ0、k是常数，h表示深度．设深度足够，有一个密度为ρ′的实心小球投入此液体中，且ρ′＞ρ0，则正确的判断是（ ）
分析：因为ρ′＞ρ0，一开始小球将下沉，因为液体密度随深度而增大（ρ=ρ0+kh），当液体的密度等于小球的密度时，小球将悬浮，据此求出h大小．
解答：解：
由题知，ρ′＞ρ0，一开始小球在液体中下沉，随着深度增加，液体的密度增加，当液体的密度等于小球的密度时，小球将悬浮，
设悬浮时的深度为h，则液体的密度ρ液=ρ0+kh，则ρ′=ρ0+kh，解得h=
．
故选D．
由题知，ρ′＞ρ0，一开始小球在液体中下沉，随着深度增加，液体的密度增加，当液体的密度等于小球的密度时，小球将悬浮，
设悬浮时的深度为h，则液体的密度ρ液=ρ0+kh，则ρ′=ρ0+kh，解得h=
| ρ′-ρ0 |
| k |
故选D．
点评：本题考查了学生对物体浮沉条件的掌握和运用，利用好悬浮条件（小球的密度和液体的密度相同）是本题的关键．
练习册系列答案
计算高手系列答案
相关题目
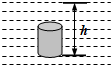（2010?静安区二模）为了研究浸没在液体中的同一物体表面受到液体的压力大小与哪些因素有关，某小组同学把高为0.2米的实心圆柱体先后竖直浸没于甲、乙、丙三种液体中进行实验，如图14所示．实验中，他们改变圆柱体下表面到液面的距离h，利用仪器测得圆柱体下（或上）表面受到液体的压强，并利用公式求得下（或上）表面受到液体的压力，记录数据如表一、表二和表三所示．（表中，F1为上表面受到液体的压力，F2为下表面受到液体的压力）表一 甲液体（ρ甲=0.8×103千克/米3）
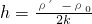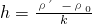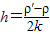处
处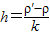
处
处