题目内容
 (2013?安顺)如图所示电路,电源电压不变.闭合开关S,当滑片P置于变阻器的b端时,电压表的示数为6V;当滑片P置于变阻器的中点时,电压表的示数变化了2V,从P置于中点开始在20s内定值电阻R1产生的热量为64J.则下列判断正确的是( )
(2013?安顺)如图所示电路,电源电压不变.闭合开关S,当滑片P置于变阻器的b端时,电压表的示数为6V;当滑片P置于变阻器的中点时,电压表的示数变化了2V,从P置于中点开始在20s内定值电阻R1产生的热量为64J.则下列判断正确的是( )分析:由电路图可知,当滑片P置于变阻器的b端时,定值电阻R1与滑动变阻器的最大阻值串联;当滑片P置于变阻器的中点时,定值电阻R1与滑动变阻器阻值的一半串联.
(1)先根据串联电路的分压特点求出当滑片P置于变阻器的中点时电压表的示数,再根据串联电路的电压特点和欧姆定律表示出电源的电压以及电路中的电流,利用电源的电压不变得出等式即可得出R1和R之间的关系;再根据Q=I2Rt表示出P置于中点时,在20s内定值电阻R1产生的热量,进一步得出R和R1的阻值,代入电源电压的表达式即可求出电源的电压;
(2)根据P=I2R和电阻之间的关系即可求出R1先后两次消耗的电功率之比.
(1)先根据串联电路的分压特点求出当滑片P置于变阻器的中点时电压表的示数,再根据串联电路的电压特点和欧姆定律表示出电源的电压以及电路中的电流,利用电源的电压不变得出等式即可得出R1和R之间的关系;再根据Q=I2Rt表示出P置于中点时,在20s内定值电阻R1产生的热量,进一步得出R和R1的阻值,代入电源电压的表达式即可求出电源的电压;
(2)根据P=I2R和电阻之间的关系即可求出R1先后两次消耗的电功率之比.
解答:解:由电路图可知,当滑片P置于变阻器的b端时,定值电阻R1与滑动变阻器的最大阻值串联;当滑片P置于变阻器的中点时,定值电阻R1与滑动变阻器阻值的一半串联.
(1)根据串联电路的分压特点可知,当滑片P置于变阻器的中点时电压表的示数为6V-2V=4V,
∵串联电路的总电压等于各分电阻两端的电压之和,
∴根据欧姆定律可得:
U=I1R1+6V,U=I2R1+4V,I1=
,I2=
=
,
∵电源的电压不变,
∴I1R1+6V=I2R1+4V
即
R1+6V=
R1+4V
简化可得:R1=R,
根据Q=I2Rt可得:
P置于中点时,在20s内定值电阻R1产生的热量:
Q1=I22R1t=(
)2R1×20s=
×R×20s=
×20s=64J,
解得:R=20Ω,即R1=20Ω,故A不正确、B正确;
电源的电压:
U=I1R1+6V=
R1+6V=
×20Ω+6V=12V,故C不正确;
(2)根据P=I2R可得:
R1先后两次消耗的电功率之比:
P1:P1′=(I1)2R1:(I2)2R1=(I1)2:(I2)2=(
)2:(
)2=9:16,故D不正确.
故选B.
(1)根据串联电路的分压特点可知,当滑片P置于变阻器的中点时电压表的示数为6V-2V=4V,
∵串联电路的总电压等于各分电阻两端的电压之和,
∴根据欧姆定律可得:
U=I1R1+6V,U=I2R1+4V,I1=
| 6V |
| R |
| 4V | ||
|
| 8V |
| R |
∵电源的电压不变,
∴I1R1+6V=I2R1+4V
即
| 6V |
| R |
| 8V |
| R |
简化可得:R1=R,
根据Q=I2Rt可得:
P置于中点时,在20s内定值电阻R1产生的热量:
Q1=I22R1t=(
| 8V |
| R |
| (8V)2 |
| R2 |
| (8V)2 |
| R |
解得:R=20Ω,即R1=20Ω,故A不正确、B正确;
电源的电压:
U=I1R1+6V=
| 6V |
| R |
| 6V |
| 20Ω |
(2)根据P=I2R可得:
R1先后两次消耗的电功率之比:
P1:P1′=(I1)2R1:(I2)2R1=(I1)2:(I2)2=(
| 6V |
| R |
| 8V |
| R |
故选B.
点评:本题考查了串联电路的特点和欧姆定律、电功率公式的灵活应用,利用好当滑片P置于变阻器的中点时电压表示数的变化的是关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
 (2013?安顺)某电饭锅设有“加热”和“保温”两档,其内部简化电路如图所示,当开关S置于“1”档时,电饭锅处于
(2013?安顺)某电饭锅设有“加热”和“保温”两档,其内部简化电路如图所示,当开关S置于“1”档时,电饭锅处于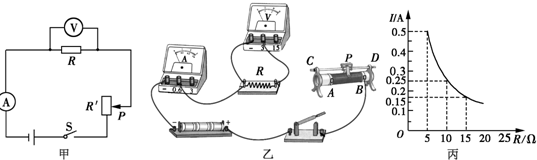
 (2013?安顺)如甲图所示的电路中,电源电压不变,R1为定值电阻.闭合开关S,将滑动变阻器R2的滑片P从a向b移动的过程中,电压表和电流表的示数变化情况如乙图所示,则R1的阻值为
(2013?安顺)如甲图所示的电路中,电源电压不变,R1为定值电阻.闭合开关S,将滑动变阻器R2的滑片P从a向b移动的过程中,电压表和电流表的示数变化情况如乙图所示,则R1的阻值为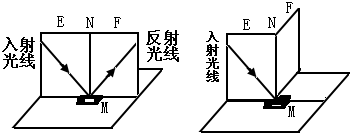 (2013?安顺)如图所示是小明同学探究反射定律的实验装置.平面镜M平放在平板上,白色硬纸板竖立在镜面上,硬纸板是由E、F两块粘接起来的,其中F可绕接缝ON转动.
(2013?安顺)如图所示是小明同学探究反射定律的实验装置.平面镜M平放在平板上,白色硬纸板竖立在镜面上,硬纸板是由E、F两块粘接起来的,其中F可绕接缝ON转动.