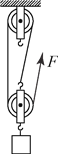题目内容
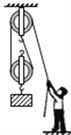
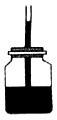
【题目】如图所示甲、乙两装置所用滑轮质量均相等,用它们分别将所挂重物在相等时间内竖直 向上匀速提升相同高度.若 G1=G2,所用竖直向上的拉力分别为 F1 和 F2,拉力做功的功 率分别为 P1 和 P2,两装置的机械效率分别为 η1 和 η2(不计绳重和 一切摩擦),则下列选项正确的是

A. F1>F2 η1<η2 P1<P2
B. F1>F2 η1=η2 P1=P2
C. F1<F2 η1<η2 P1=P2
D. F1<F2 η1=η2 P1>P2
【答案】B
【解析】因为动滑轮重相同,提升的物体重和高度相同,W额=G轮h,W有用=G物h,所以利用滑轮组做的有用功相同、额外功相同,总功相同;由η=W有/W总×100%可知,机械效率相同,η1 =η2;又因为所用时间相同,由P=W/t可知,拉力做功的功率P1 =P2 ,故A错误,B正确;不计绳重及摩擦,由滑轮组的结构知道承担物重的绳子股数n,所以拉力F =1/n(G+G动)/n,因为n1 =2,n2 =3,所以绳子受到的拉力分别为:F1 =(G1 +G动)/2,F2 =(G2 +G动)/3,G1 =G2 ,故F1>F2,故CD错误,故选B。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目