题目内容
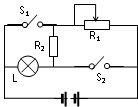 如图所示电路中,电源电压不变,灯的电阻不随温度变化,当开关S1、S2都闭合时,灯L正常发光,此时,R1>R2,R1消耗的功率为36瓦.当开关S1、S2都断开时,保持R1的电阻不变,灯L的功率为其额定功率的1/4,R2消耗的功率为2瓦.已知R1的最大电阻为R2的10倍.求:
如图所示电路中,电源电压不变,灯的电阻不随温度变化,当开关S1、S2都闭合时,灯L正常发光,此时,R1>R2,R1消耗的功率为36瓦.当开关S1、S2都断开时,保持R1的电阻不变,灯L的功率为其额定功率的1/4,R2消耗的功率为2瓦.已知R1的最大电阻为R2的10倍.求:(1)灯L的额定功率.
(2)当开关S1、S2都断开时,R1的最大功率.
分析:电源电压U不变,当S1、S2都闭合时,灯泡L与R1、R2并联,灯泡正常发光,此时灯泡的功率就是额定功率,由P=
可求表示出R1消耗的功率;
当S1、S2都断开时,灯泡L与电阻R1、R2串联;根据欧姆定律用电阻和电源电压表示出电路总电流;根据公式P=I2R可求出R1的最大功率.
| U2 |
| R |
当S1、S2都断开时,灯泡L与电阻R1、R2串联;根据欧姆定律用电阻和电源电压表示出电路总电流;根据公式P=I2R可求出R1的最大功率.
解答:解:(1)当开关都闭合时,三者是并联关系,设电源电压为U(即电灯的额定电压为U),电灯的额定电流为I,则有
=36W…①
当开关都断开时,三者是串联关系,由于此时灯泡是额定功率的1/4,所以电流是额定电流的一半,电压是额定电压的一半,电阻R1、R2两端的电压之和为
,所以有关系式
=
(R1+R2)…②
且此时R2的功率为2W,有关系式(
)2R2=2W…③
由①②③联立解方程组,消掉U和I,则可以得到
(2R1-R2)(R1-2R2)=0.
因为题目给定条件R1>R2,所以有R1=2R2.
根据开关都断开可得,R1、R2两端电压之和为
,电阻比为2:1,所以电压比也为2:1,即R2两端电压为
.因为流过的电流为
I,所以根据功率为2W,有
×
I=2W,解得U×I=24W,故灯泡的额定功率为24W.
(2)因为开关都断开时,灯泡的实际功率为
×24W=6W,R2消耗的功率为2W,所以由P=I2R可得,RL:R2=3:1,那么
R1的功率P1=(
)2R1=(
)2=
=
当4R2=R1时,R1的功率最大,因此R1的最大功率为P1=
=
=
×24W=4.5W.
答:(1)灯L的额定功率24W.
(2)当开关S1、S2都断开时,R1的最大功率为4.5W.
| U2 |
| R1 |
当开关都断开时,三者是串联关系,由于此时灯泡是额定功率的1/4,所以电流是额定电流的一半,电压是额定电压的一半,电阻R1、R2两端的电压之和为
| U |
| 2 |
| U |
| 2 |
| I |
| 2 |
且此时R2的功率为2W,有关系式(
| I |
| 2 |
由①②③联立解方程组,消掉U和I,则可以得到
(2R1-R2)(R1-2R2)=0.
因为题目给定条件R1>R2,所以有R1=2R2.
根据开关都断开可得,R1、R2两端电压之和为
| u |
| 2 |
| U |
| 6 |
| 1 |
| 2 |
| U |
| 6 |
| 1 |
| 2 |
(2)因为开关都断开时,灯泡的实际功率为
| 1 |
| 4 |
R1的功率P1=(
| U |
| RL+R1+R2 |
| U |
| 4R2+R1 |
| U2 | ||
|
| U2 | ||
|
当4R2=R1时,R1的功率最大,因此R1的最大功率为P1=
| U2 |
| 16R2 |
| U2 | ||
|
| 3 |
| 16 |
答:(1)灯L的额定功率24W.
(2)当开关S1、S2都断开时,R1的最大功率为4.5W.
点评:本题考查电压、电阻、电流、实际功率等的计算,关键是公式及其变形的灵活运用,难点是对电路的正确分析以及利用完全平方求最大值.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 6、如图所示电路中,电源电压保持不变,闭合开关S1后,当开关S2由1位置转换到2位置时,电压表和电流表的示数变化情况是( )
6、如图所示电路中,电源电压保持不变,闭合开关S1后,当开关S2由1位置转换到2位置时,电压表和电流表的示数变化情况是( ) 如图所示电路中,电源电压为3V,发现L1、L2不亮,用电压表测量,Uab=0V,Ubc=3V,则可能是( )
如图所示电路中,电源电压为3V,发现L1、L2不亮,用电压表测量,Uab=0V,Ubc=3V,则可能是( ) 如图所示电路中,电源电压为6V,且保持不变,电阻R1=5Ω,闭合开关S1,断开开关S2,若将滑动变阻器的滑片P移动到b端时,测得R1两端电压U1=1.2V,求:
如图所示电路中,电源电压为6V,且保持不变,电阻R1=5Ω,闭合开关S1,断开开关S2,若将滑动变阻器的滑片P移动到b端时,测得R1两端电压U1=1.2V,求: 如图所示电路中,电源电压保持不变,电阻R1的阻值为20Ω,闭合开关S.电流表Al的示数为0.3A,电流表A2的示数为0.1A,则电阻R2=
如图所示电路中,电源电压保持不变,电阻R1的阻值为20Ω,闭合开关S.电流表Al的示数为0.3A,电流表A2的示数为0.1A,则电阻R2=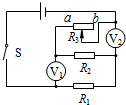 如图所示电路中,电源两端电压一定,闭合开关S,当滑动变阻器的滑片P在a端时,电压表V1和电压表V2的示数分别为U1、U2,R1消耗的功率为10W;当滑动变阻器的滑片P在b端时,电压表V2的示数为U2′.
如图所示电路中,电源两端电压一定,闭合开关S,当滑动变阻器的滑片P在a端时,电压表V1和电压表V2的示数分别为U1、U2,R1消耗的功率为10W;当滑动变阻器的滑片P在b端时,电压表V2的示数为U2′.