题目内容
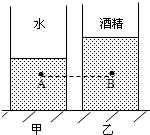 如图所示,甲、乙两个完全相同的圆柱形容器放在水平地面上,它们重2N,底面积为0.01m2,容器高0.5m.现在两个容器中分别倒入一定量的水和酒精,使得两容器中离底部0.3m处A、B两点的压强都为980Pa,求:
如图所示,甲、乙两个完全相同的圆柱形容器放在水平地面上,它们重2N,底面积为0.01m2,容器高0.5m.现在两个容器中分别倒入一定量的水和酒精,使得两容器中离底部0.3m处A、B两点的压强都为980Pa,求:
(1)A点离液面的距离hA.
(2)甲容器对水平地面的压力F甲.
(3)为使水和酒精对甲、乙两个容器底压强相等,小华和小芳设计了不同的方法,如下表所示.
| 设计的方案 | |
| 小华 | 分别在甲、乙两个容器中倒入相同深度的水和酒精. |
| 小芳 | 分别在甲容器中抽取、乙容器中倒入相同深度的水和酒精. |
解:(1)∵p=ρgh,
∴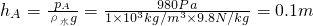 ;
;
(2)甲容器装水重:
G甲=ρ水V水g
=1.0×103kg/m3×0.01m2×(0.1m+0.3m)×9.8N/kg
=39.2N,
甲容器对水平地面的压力:
F=G甲+G容=39.2N+2N=41.2N;
(3)小芳同学设计的方法可行,
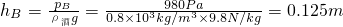
由题知:ρ水g(h甲-h)=ρ酒精g(h乙+h)
即:1×103kg/m3×9.8N/kg×(0.4m-h)=0.8×103kg/m3×9.8N/kg×(0.425m+h)
解得:h=0.03m.
答:(1)A点离液面的距离为0.1m;
(2)甲容器对水平地面的压力为41.2N;
(3)小芳同学设计的方法可行,该方法中的深度为0.03m.
分析:(1)知道A点受到水的压强和水的密度,利用液体压强公式求A点所处的深度;
(2)求出水的深度,知道底面积,可以计算水的体积,再利用密度公式和重力公式求容器内水重,可进一步求出水平地面受到的压力F=G(容器重加上水重);
(3)知道AB两点受到液体的压强相等,AB到容器底等高,由此可知此时甲容器底受到水的压强比乙容器底受到的酒精的压强大,而小华的设计方案使得甲容器底受到的压强更大,不可行;小芳的设计方案可行.
设该方法中的深度为h,根据两容器底受到的压强相等列方程求出h的大小.
点评:本题考查了密度公式、重力公式、液体压强公式,涉及到实验方案的设计,属于难题;理解深度h的含义(从该点到水面的垂直距离)是本题的关键.
∴
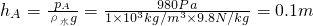 ;
;(2)甲容器装水重:
G甲=ρ水V水g
=1.0×103kg/m3×0.01m2×(0.1m+0.3m)×9.8N/kg
=39.2N,
甲容器对水平地面的压力:
F=G甲+G容=39.2N+2N=41.2N;
(3)小芳同学设计的方法可行,
由题知:ρ水g(h甲-h)=ρ酒精g(h乙+h)
即:1×103kg/m3×9.8N/kg×(0.4m-h)=0.8×103kg/m3×9.8N/kg×(0.425m+h)
解得:h=0.03m.
答:(1)A点离液面的距离为0.1m;
(2)甲容器对水平地面的压力为41.2N;
(3)小芳同学设计的方法可行,该方法中的深度为0.03m.
分析:(1)知道A点受到水的压强和水的密度,利用液体压强公式求A点所处的深度;
(2)求出水的深度,知道底面积,可以计算水的体积,再利用密度公式和重力公式求容器内水重,可进一步求出水平地面受到的压力F=G(容器重加上水重);
(3)知道AB两点受到液体的压强相等,AB到容器底等高,由此可知此时甲容器底受到水的压强比乙容器底受到的酒精的压强大,而小华的设计方案使得甲容器底受到的压强更大,不可行;小芳的设计方案可行.
设该方法中的深度为h,根据两容器底受到的压强相等列方程求出h的大小.
点评:本题考查了密度公式、重力公式、液体压强公式,涉及到实验方案的设计,属于难题;理解深度h的含义(从该点到水面的垂直距离)是本题的关键.

练习册系列答案
相关题目
 5、如图所示,甲、乙两个房间里的相同的两壶水放在相同的电炉上都已烧开,我们可以根据所观察的
5、如图所示,甲、乙两个房间里的相同的两壶水放在相同的电炉上都已烧开,我们可以根据所观察的 (2013?亳州模拟)如图所示,甲、乙两个均匀实心正方体分别放置在水平地面上,且它们各自对地面的压强相等.若分别在两个正方体的上部,沿水平方向截去相同高度后,则甲、乙的剩余部分对地面的压强P以及剩余部分质量m的大小关系为( )
(2013?亳州模拟)如图所示,甲、乙两个均匀实心正方体分别放置在水平地面上,且它们各自对地面的压强相等.若分别在两个正方体的上部,沿水平方向截去相同高度后,则甲、乙的剩余部分对地面的压强P以及剩余部分质量m的大小关系为( ) (2013?广安)用四只完全相同的滑轮和两根相同的绳子组成如图所示的甲、乙两个滑轮组,分别将两个相同的钩码提升10cm,若不计绳子与滑轮的摩擦,
(2013?广安)用四只完全相同的滑轮和两根相同的绳子组成如图所示的甲、乙两个滑轮组,分别将两个相同的钩码提升10cm,若不计绳子与滑轮的摩擦, 如图所示,甲、乙两个电磁铁靠近放置,a、b和f、d分别接电源,那么( )
如图所示,甲、乙两个电磁铁靠近放置,a、b和f、d分别接电源,那么( ) 用四只完全相同的滑轮和两根相同的绳子组成如图所示的甲、乙两个滑轮组,不计绳子与滑轮的摩擦,则( )
用四只完全相同的滑轮和两根相同的绳子组成如图所示的甲、乙两个滑轮组,不计绳子与滑轮的摩擦,则( )