题目内容
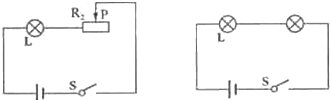
 如图所示,灯L标有“6V 3W”,滑动变阻器的最大电阻为24欧.当电键S断开,变阻器的滑片P滑至a端时,灯L正常发光,如果灯L的电阻不变,当P滑至b端时,电流表的示数为
如图所示,灯L标有“6V 3W”,滑动变阻器的最大电阻为24欧.当电键S断开,变阻器的滑片P滑至a端时,灯L正常发光,如果灯L的电阻不变,当P滑至b端时,电流表的示数为0.17
0.17
安,小灯的功率为0.33
0.33
瓦.此时闭合电键S,则电流表的示数为0.25A
0.25A
,灯L的发光情况是不发光
不发光
.(保留两位小数)分析:(1)当电键S断开,变阻器的滑片P滑至a端时,电路为灯泡L的简单电路,根据灯泡正常发光时的电压和额定电压相等可知电源的电压;当P滑至b端时,灯泡与滑动变阻器的最大阻值串联,电流表测电路中的电流,根据P=
求出灯泡的电阻,再根据电阻的串联和欧姆定律求出此时电路中的电流,最后根据P=I2R求出灯泡的实际功率;
(2)此时闭合电键S时,灯泡被短路、不能发光,电路为滑动变阻器最大阻值的简单电路,根据欧姆定律求出电流表的示数.
| U2 |
| R |
(2)此时闭合电键S时,灯泡被短路、不能发光,电路为滑动变阻器最大阻值的简单电路,根据欧姆定律求出电流表的示数.
解答:解:(1)当电键S断开,变阻器的滑片P滑至a端时,电路为灯泡L的简单电路,
∵灯泡正常发光,
∴电源的电压U=UL额=6V;
当P滑至b端时,灯泡与滑动变阻器的最大阻值串联,电流表测电路中的电流,
根据P=
可得:
灯泡的电阻RL=
=
=12Ω,
∵串联电路的总电阻等于各分电阻之和,
∴根据欧姆定律可得,此时电路中的电流I=
=
=
A≈0.17A,
灯泡的实际功率PL=I2RL=(
A)2×12Ω≈0.33W;
(2)此时闭合电键S时,灯泡被短路、不能发光,电路为滑动变阻器最大阻值的简单电路,
电流表的示数I′=
=
=0.25A.
故答案为:0.17;0.33;0.25;不发光.
∵灯泡正常发光,
∴电源的电压U=UL额=6V;
当P滑至b端时,灯泡与滑动变阻器的最大阻值串联,电流表测电路中的电流,
根据P=
| U2 |
| R |
灯泡的电阻RL=
| U2L额 |
| PL额 |
| (6V)2 |
| 3W |
∵串联电路的总电阻等于各分电阻之和,
∴根据欧姆定律可得,此时电路中的电流I=
| U |
| RL+R滑 |
| 6V |
| 12Ω+24Ω |
| 1 |
| 6 |
灯泡的实际功率PL=I2RL=(
| 1 |
| 6 |
(2)此时闭合电键S时,灯泡被短路、不能发光,电路为滑动变阻器最大阻值的简单电路,
电流表的示数I′=
| U |
| R滑 |
| 6V |
| 24Ω |
故答案为:0.17;0.33;0.25;不发光.
点评:本题考查了串联电路的特点和欧姆定律、电功率公式的灵活运用,关键是知道灯泡正常发光时的电压和额定电压相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,灯L标有“6V 3W”字样,电源电压1OV,闭合开关S,调节滑动变阻器使灯L正常发光(电源电压和灯丝电阻保持不变).求:
如图所示,灯L标有“6V 3W”字样,电源电压1OV,闭合开关S,调节滑动变阻器使灯L正常发光(电源电压和灯丝电阻保持不变).求: 如图所示,灯L标有“6伏3.6瓦”字样,滑动变阻器R最大值为50欧,电压U为6伏.则下列说法正确的是( )
如图所示,灯L标有“6伏3.6瓦”字样,滑动变阻器R最大值为50欧,电压U为6伏.则下列说法正确的是( ) (2009?闸北区二模)如图所示,灯L标有“6V 3W”,滑动变阻器的最大电阻为24欧.当电键S断开,变阻器的滑片P滑至a端时,灯L正常发光,此时灯L的电阻为
(2009?闸北区二模)如图所示,灯L标有“6V 3W”,滑动变阻器的最大电阻为24欧.当电键S断开,变阻器的滑片P滑至a端时,灯L正常发光,此时灯L的电阻为 如图所示,灯L标有“6V 3W”字样,开关S既可以与a连接,也可以与b连接,电源电压恒定为9V,R2的阻值为18Ω,不考虑温度对灯泡电阻的影响,当S接b时,灯 L恰好能正常发光,则电阻R1的阻值为
如图所示,灯L标有“6V 3W”字样,开关S既可以与a连接,也可以与b连接,电源电压恒定为9V,R2的阻值为18Ω,不考虑温度对灯泡电阻的影响,当S接b时,灯 L恰好能正常发光,则电阻R1的阻值为