题目内容
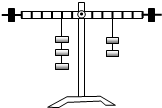 在探究“杠杆的平衡条件”实验中.
在探究“杠杆的平衡条件”实验中.(1)把杠杆的中点支在支架上,调节平衡螺母,使杠杆在
水平
水平
位置平衡;(2)杠杆平衡后,在往后的实验过程中
不能
不能
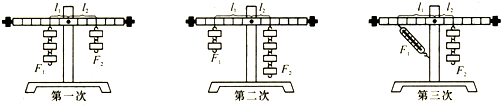
(选填“能”或“不能”)再调节两侧的平衡螺母;(3)改变力和力臂的数值,做了三次实验,并将实验数据记录在下表中:
| 实验次数 | 动力F1/N | 动力臂l1/cm | 阻力F2/N | 阻力臂l2/cm |
| 1 | 0.5 | 20 | 1 | 10 |
| 2 | 1 | 15 | 1.5 | 10 |
| 3 | 2 | 15 | 1.5 | 20 |
F1l1=F2l2
F1l1=F2l2
;(4)实验中多次测量的目的是
排除偶然性,得到普遍的规律
排除偶然性,得到普遍的规律
.(5)杠杆平衡后,如图所示,在两侧钩码下各减少一个相同的钩码,则杠杆的
左端
左端
下沉(选填“左端”、“右端”).分析:(1)实验中为了便于测量力臂,应调节杠杆在水平位置平衡;
(2)实验前通过调节平衡螺母使杠杆平衡;实验中通过调节钩码的个数和位置使杠杆平衡;
(3)分析表格中数据得出杠杆平衡条件:F1l1=F2l2;
(4)实验中为了得出普遍性规律,避免偶然性,要进行多次测量;
(5)分别计算两边力和力臂的大小,进行比较,则杠杆向乘积较大的一侧倾斜.
(2)实验前通过调节平衡螺母使杠杆平衡;实验中通过调节钩码的个数和位置使杠杆平衡;
(3)分析表格中数据得出杠杆平衡条件:F1l1=F2l2;
(4)实验中为了得出普遍性规律,避免偶然性,要进行多次测量;
(5)分别计算两边力和力臂的大小,进行比较,则杠杆向乘积较大的一侧倾斜.
解答:解:(1)把杠杆的中点支在支架上,调节平衡螺母,使杠杆在水平位置平衡;
(2)杠杆平衡后,在往后的实验过程中不能再调节两侧的平衡螺母,应通过调节钩码的个数和位置使杠杆平衡;
(3)由表格中数据,
1、0.5N×20cm=1N×10cm=10N?cm;
2、1N×15cm=1.5N×10cm=15N?cm;
3、2N×15cm=1.5N×20cm=30N?cm;
可知杠杆的平衡条件为;F1l1=F2l2;
(4)实验中多次测量是为了排除偶然性,得到普遍的规律;
(5)都增加一个钩码后,左边=4G×2L=8GL,右边=3G×3L=9GL;
故答案为:(1)水平;(2)不能;(3)F1l1=F2l2;(4)排除偶然性,得到普遍的规律;(5)左端.
(2)杠杆平衡后,在往后的实验过程中不能再调节两侧的平衡螺母,应通过调节钩码的个数和位置使杠杆平衡;
(3)由表格中数据,
1、0.5N×20cm=1N×10cm=10N?cm;
2、1N×15cm=1.5N×10cm=15N?cm;
3、2N×15cm=1.5N×20cm=30N?cm;
可知杠杆的平衡条件为;F1l1=F2l2;
(4)实验中多次测量是为了排除偶然性,得到普遍的规律;
(5)都增加一个钩码后,左边=4G×2L=8GL,右边=3G×3L=9GL;
故答案为:(1)水平;(2)不能;(3)F1l1=F2l2;(4)排除偶然性,得到普遍的规律;(5)左端.
点评:探究杠杆平衡条件时,使杠杆在水平位置平衡,便于测量力臂大小,为得出普遍性的规律,应多次几组数据进行分析.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
甲乙两个实验小组在探究“杠杆的平衡条件”时,分别得到下面两组数据和结论
| 甲 组 | |||||
| 次数 | 动力 | 动力臂 | 阻力 | 阻力臂 | |
| 1 | 7 | 4 | 2 | 14 | |
| 2 | 6 | 4 | 8 | 3 | |
| 3 | 4 | 5 | 2 | 10 | |
| 结论 | 动力*动力臂=阻力*阻力臂 | ||||
| 乙 组 | |||||
| 次数 | 动力 | 动力臂 | 阻力 | 阻力臂 | |
| 1 | 3 | 4 | 4 | 3 | |
| 2 | 4 | 5 | 5 | 4 | |
| 结论 | 动力+动力臂=阻力+阻力臂 | ||||
他们在交流时,乙组发现了自己实验结论的错误和出现错误的原因。你认为乙组出现错误的原因有哪些?请找出两条.
原因①:________________________________________________________________.
原因②:________________________________________________________________.