��Ŀ����
����Ŀ���ڡ�̽�������ֵĻ�еЧ�ʡ�ʱ��ijС���������ز�ͬ�����������ֽ�������ͼ��ʾ�����β��������ݼ�¼���£�
ʵ����� | ������/N | ��������/N | ����/N | ���������ĸ߶�/m | �������ƶ��ľ���/m | ���ù�/J | �ܹ�/J | ��еЧ��/% |
�� | 4 | 0.5 | 2.3 | 0.2 | 0.4 | 0.8 | 0.92 | 87.0 |
�� | 4 | 0.9 | 2.5 | 0.2 | 0.4 | 0.8 | 1.0 | |
�� | 6 | 0.5 | 3.3 | 0.2 | 0.4 |

��1����ɱ����пհ״��ļ��㣬ֱ�����ڱ���Ŀհ״���
��2��ͨ���Ƚ� ����ʵ�����ݣ�ѡ��ʵ����ţ�����֪�����ֵĻ�еЧ���붯���ֵ����� ��ѡ��йء����ء�����
��3��С����Ϊ��ͬһ����е�����Ļ�еЧ����һ����ֵ����ͨ���Ƚ� ����ʵ�����ݣ�ѡ��ʵ����ţ�����֪���Ĺ۵��� �ģ�ѡ���ȷ��������
��4���ڶ���ʵ���У������������õ�ʱ��Ϊ1.5s�������Ĺ���Ϊ W��
��5�������ʵ������У�С��ͬѧб���������ɲ����ƣ�������Ļ�еЧ�ʻ� ����ѡ������С�䡱��
���𰸡���1��1.2��1.32��90.9����2������ڣ��йأ���3������ۣ�����3��0.67����5����С��
��������
�����������1�����ù����ڹ����������������߶ȵij˻�����W����=Gh���ܹ����������Ͳ������ƶ�����ij˻�����W��=FS����еЧ�ʵ������ù����ܹ��ı�ֵ������=![]() ��100%��
��100%��
��2���о������ֻ�еЧ���붯�������������Ƿ��й�ʱ��Ӧ�������������������ͬ���ı䶯����������
��3��ͬһ����е����������ϲ��䣬�����������������仯ʱ�����ù����ܹ���ռ�ñ�ֵ�ͱ仯����еЧ��Ҳ�ͱ仯��
��4�������Ĺ���Ӧ���ö��������Ĺ�������������ʱ�䣬�����ù�ʽP=![]() �����㣻
�����㣻
��5���ж������ı仯���ó��ܹ��ı仯���Ӷ��ɸ��ݻ�еЧ�ʹ�ʽ�ó������еЧ�ʵı仯��
�⣺��1���ڶ������ݣ���=![]() ��100%=
��100%=![]() ��100%=80%��
��100%=80%��
��3�������У����ù�W����=Gh=6N��0.2m=1.2J��
�ܹ�W��=FS=3.3N��0.4m=1.32J��
��еЧ�ʦ�=![]() ��100%=
��100%=![]() ��100%��90.9%��
��100%��90.9%��
��2���٢�����ʵ���У������������ͬ�������ֵ�������ͬ����еЧ��Ҳ��ͬ�����̽�����ǻ�еЧ���붯�������صĹ�ϵ��
��3���ȽϢ٢ۣ�ͬһ����е���������������䣬����������������ͬʱ����еЧ��Ҳ��ͬ���������Խ�أ���еЧ��Խ��֪С���Ĺ۵��Ǵ���ģ�
��4���ɱ���������֪�����������Ĺ�W=Fs=2.5N��0.4m=1J��
�����Ĺ���Ϊ��P=![]() =
=![]() ��0.67W��
��0.67W��
��5�������ʵ������У�С��ͬѧб���������ɲ����ƣ���������ƫ���ܹ�ƫ���ɹ�ʽ��=![]() ��֪������Ļ�еЧ�ʻ�ƫС��
��֪������Ļ�еЧ�ʻ�ƫС��
�ʴ�Ϊ����1��1.2��1.32��90.9����2������ڣ��йأ���3������ۣ�����3��0.67����5����С��

����Ŀ��С��Ϊ��̽��������ˮ�в�ͬ������ܸ����仯�������ͼ��ʾ����һ���ڵ��ɲ������µ�Բ��������黺������ˮ�У�ˮ�㹻�����Բ����Ӵ�������֮ǰ���ֱ����Բ�����±��������IJ�ͬ���h�͵��ɲ�������Ӧ��ʾ��F��ʵ�����������
���� | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
h��cm�� | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
F��N�� | 6.75 | 6.25 | 5.75 | 5.25 | 4.75 | 4.25 | 4.25 |
��1����������ʵ�����ݣ����Եó������� N����4��ʵ��ʱ�������ܵ��ĸ��� N��
��2���������е�1�е���5�����ݣ�˵�� ��
��3��ʵ��ʱӦ�Ȳ�������������ٷ���ˮ�в⸡�����ı��Ⱥ�˳���ʹ�����IJ������ƫ ��������С����
��4��ͼ������ȷ��ӳ���ɲ�����ʾ��F��Բ�����±��浽ˮ�����h��ϵ��ͼ����
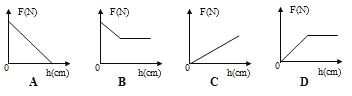
��5��Բ������ܶ�Ϊ kg/m3��

