题目内容
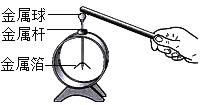
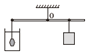
【题目】如图所示,轻质杆可绕O点转动。分别将质量相同的纯金块、纯银块、金银制作的王冠悬挂于杆的最左端并浸没水中,将质量与王冠相同的重物对应地悬挂在杆上的A、B、C处(图中未标出),杆恰好在水平位置平衡。测得A、C两点间的距离为7cm,B、C两点间的距离为3cm。则王冠中金和银的质量比为( )
A. 3:7 B. 7:3 C. 2:5 D. 5:2
【答案】A
【解析】
先利用V=![]() 判断三者体积关系,根据阿基米德原理和杠杆平衡条件可得出重物对应地悬挂在杆上的A、B、C的位置,然后分别列出三者悬挂于杆的最左端并浸没水中时的等量关系式,结合数学知识将这三个方程进行整理即可得出王冠中金和银的质量之比。
判断三者体积关系,根据阿基米德原理和杠杆平衡条件可得出重物对应地悬挂在杆上的A、B、C的位置,然后分别列出三者悬挂于杆的最左端并浸没水中时的等量关系式,结合数学知识将这三个方程进行整理即可得出王冠中金和银的质量之比。
设纯金块、纯银块、金银制作的王冠以及重物的质量为m,
纯金块、纯银块、金银制作的王冠的密度分别为ρ1、ρ2、ρ3,体积分别为V1、V2、V3,
由于ρ1>ρ3>ρ2,根据V=![]() 可知,三者的体积关系:V1<V3<V2,
可知,三者的体积关系:V1<V3<V2,
浸没在水中时,三者排开水的体积与各自的体积相等,
根据F浮=ρ水gV排可知,三者的浮力关系:F浮1<F浮3<F浮2,
当质量相同(重力相同)的纯金块、纯银块、金银制作的王冠悬挂于杆的最左端并分别浸没水中时,杆的最左端受到的拉力:F拉=G﹣F浮,由于F浮1<F浮3<F浮2,则F拉1>F拉3>F拉2,且左边拉力的力臂相同,
根据杠杆平衡条件可知,相同的重物对应地悬挂在杆上的A、B、C处,如下图所示:

根据阿基米德原理和杠杆平衡条件得,当纯金块悬挂于杆的最左端并浸没水中时有:
(mg﹣ρ水gV1)LOD=mg(LOB+LBC+LAC)﹣﹣﹣﹣﹣①
当纯银块悬挂于杆的最左端并浸没水中时有:
(mg﹣ρ水gV2)LOD=mgLOB ﹣﹣﹣﹣﹣﹣②
当金银制作的王冠悬挂于杆的最左端并浸没水中时有:
(mg﹣ρ水gV3)LOD=mg(LOB+LBC)﹣﹣﹣﹣﹣﹣③
用①﹣②得,(ρ水gV2﹣ρ水gV1)LOD=mg(LBC+LAC)﹣﹣﹣﹣﹣﹣④
用③﹣②得,(ρ水gV2﹣ρ水gV3)LOD=mgLBC﹣﹣﹣﹣﹣﹣⑤
用④÷⑤得, ![]() =
=![]() =
=![]() =
=![]() ,
,
化简整理得,10V3﹣3V1﹣7V2=0﹣﹣﹣﹣﹣⑥
设王冠中金和银的质量分别为m1、m2,
则王冠的体积:V3=![]() +
+ ![]() ﹣﹣﹣﹣﹣⑦
﹣﹣﹣﹣﹣⑦
纯金块的体积:V1=![]() ﹣﹣﹣﹣﹣﹣﹣⑧
﹣﹣﹣﹣﹣﹣﹣⑧
纯银快的体积:V2=![]() ﹣﹣﹣﹣﹣﹣﹣﹣﹣⑨
﹣﹣﹣﹣﹣﹣﹣﹣﹣⑨
将⑦⑧⑨代入⑥整理得,![]() +
+![]() =0,
=0,
由于ρ1>ρ2>0,所以,10m1﹣3m=0;10m2﹣7m=0;
解得:m1=![]() m;m2=
m;m2=![]() m;
m;
则王冠中金和银的质量之比:
m1:m2=![]() m:
m:![]() m=3:7。
m=3:7。
故选:A。

 春雨教育同步作文系列答案
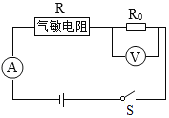
春雨教育同步作文系列答案【题目】在测量动滑轮机械效率的实验中,小明用如图所示的动滑轮提升钩码,改变钩码的数量,正确操作所得实验数据如下:
实验 序号 | 钩码重 G/N | 钩码上升 高度h/cm | 拉力 F/N | 绳端移动的距离s/cm | 机械效率 |
① | 1.0 | 20.0 | 0.7 | 40.0 | 71.4% |
② | 2.0 | 20.0 | 1.2 | 40.0 | |
③ | 3.0 | 20.0 | 1.7 | 40.0 | 88.2% |

(1)实验时,用手_____匀速拉动弹簧测力计,使挂在动滑轮上的钩码缓缓上升。
(2)第②次实验测得的动滑轮的机械效率为_____%(计算结果的位数与表中机械效率位数一致)。
(2)由表中数据分析可知,同一动滑轮的机械效率由_____决定的。
(4)不计绳重及摩擦阻力,则该动滑轮的自重为_____N。