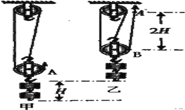��Ŀ����
����Ŀ����ͼ����ʾ��һ�����˽��뵽һ����ֱ���뺣��Բ���θֻ�Ͳ�ĵײ���ҵʱ����ˮ�dz����ֻ�Ͳ�ϲ�ˮ������2�����λ��ͻȻ���Σ���խ�ĵط�ֻ��3��5cm�����˱����ֻ�Ͳ�ײ��� 
��1��ͼ���иֻ�Ͳ��խ���ܵ���ˮ��ѹǿ�Ƕ��٣�
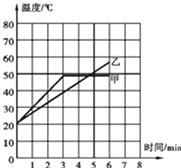
��2��Ϊ�˽����˾ȳ�����Ԯ��Ա����ֻ�Ͳ�¶�����һ���ˮ���жϣ���֪�ֻ�Ͳ��ͬ�и�������ˮ�����˵ȵ�����Ϊ2.0��106N������ˮ�е����Ϊ40m3 �� �������ػ��������ǣ����رۻ������ϵĸ����Ʒ���ͼ����ʾ������³��ܵ������仯��ΧΪ���٣�����ˮ���ܶ�ȡ1.0��103kg/m3 �� gȡ10N/kg�������Ƿ��ˡ�ˮ���ȵ�Ӱ�죬�����֡������������ؼ�Ħ�������Բ��ƣ�
���𰸡�
��1���⣺�ֻ�Ͳ��խ���ܵ���ˮ��ѹǿ��
p=��gh=1.0��103 kg/m3��10N/kg��2m=2��104Pa
��2���⣺�����֪�������֡������������ؼ�Ħ�������Բ��ƣ���ͼ��֪��n=4��
���ֻ�Ͳ��ͬ�и�������ˮ��ȫ��¶��ˮ�棨�����ܸ������ã�ʱ��
��ʱ���³��ܵ����������F��= ![]() ��G=
��G= ![]() ��2.0��106N=5��105N��
��2.0��106N=5��105N��
���ֻ�Ͳ��ͬ�и�������ˮ��δ¶��ˮ�棨����û��ˮ�У�ʱ��
�ֻ�Ͳ��ˮ���ܵ��ĸ�����F��=��ˮV��g=1.0��103kg/m3��40m3��10N/kg=4��105N��
��ʱ���³��ܵ�������С����FС= ![]() ��G��F����=
��G��F����= ![]() ����2��106N��4��105N��=4��105N��
����2��106N��4��105N��=4��105N��
���ԣ����³��ܵ�������ΧΪ��4��105N��5��105N
����������1�����ݹ�ʽp=��gh�����ˮ��ѹǿ����2������ֻ�Ͳ��ͬ�и�������ˮ��δ¶��ˮ��ʱ���ܵĸ�������F= ![]() ��G��F���������С�����������ȫ��¶��ˮ��ʱ���������ܵ�������������������ݴ�ȷ�����³��ܵ������仯��Χ��
��G��F���������С�����������ȫ��¶��ˮ��ʱ���������ܵ�������������������ݴ�ȷ�����³��ܵ������仯��Χ��
�����㾫��������Һ���ѹǿ�ļ��������С�ļ������Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪Һ���ڲ�ѹǿ�Ĺ�ʽ��p=��gh ��ָ�ܶ�,��λkg/m3,g=9.8N/kg, hָ���,��λ:m,ѹǿ��λ(Pa) ע�⣺h ָҺ�����ȣ���ij�㵽Һ��ľ��룻�����Ĺ�ʽΪ��F��= G�� =��Һgv����

 ��У����ϵ�д�
��У����ϵ�д�