题目内容
 如图所示电路,电源电压保持不变,灯L的电阻不随温度变化.当开关S1断开、S2闭合时,电压表V1的示数为U1,电流表的示数为I1;当两个开关都断开时,电压表V2的示数为U2,电阻R1的功率P1=2W;当只闭合S1时,灯泡L正常发光,电流表的示数为I3.已知U1:U2=5:4,I1:I3=2:3.求:
如图所示电路,电源电压保持不变,灯L的电阻不随温度变化.当开关S1断开、S2闭合时,电压表V1的示数为U1,电流表的示数为I1;当两个开关都断开时,电压表V2的示数为U2,电阻R1的功率P1=2W;当只闭合S1时,灯泡L正常发光,电流表的示数为I3.已知U1:U2=5:4,I1:I3=2:3.求:(1)阻值R1与R2之比;
(2)灯L的额定功率PL.
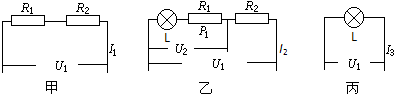
分析:先画出三种情况的等效电路图:①当开关S1断开、S2闭合时,电阻R1和R2串联,电压表V1测量的是电阻R1和R2两端的电压,电流表A测量的是整个电路中的电流;电压表V1的示数为U1,电流表A示数为I1.
②当开关S1和S2都断开时,电阻R1、R2和灯L串联,电压表V1测量的是电阻R1、R2和灯L两端的电压,电压表V2测量的是R2和灯L两端的电压,电流表A测量的是整个电路中的电流;电压表V2的示数为U2,电阻R1的功率P1=2W.
③当只闭合开关S1时,电路中只有灯泡L,并且灯泡L正常发光,电压表V1测量的是灯L两端的电压.
(1)根据欧姆定律和串联电路的电压特点,结合图甲和图乙中U1:U2=5:4列出一个电阻的比值关系式;再结合 图甲和图丙中I1:I3=2:3列出一个电阻的比值关系式,结合两个关系式便可以计算出阻值R1与R2之比.
(2)根据欧姆定律结合图乙和图丙求出两者的电流之比,再根据P=I2R计算出电阻R1的功率P1与灯L的额定功率PL之比,从而可以计算出灯L的额定功率PL.
②当开关S1和S2都断开时,电阻R1、R2和灯L串联,电压表V1测量的是电阻R1、R2和灯L两端的电压,电压表V2测量的是R2和灯L两端的电压,电流表A测量的是整个电路中的电流;电压表V2的示数为U2,电阻R1的功率P1=2W.
③当只闭合开关S1时,电路中只有灯泡L,并且灯泡L正常发光,电压表V1测量的是灯L两端的电压.
(1)根据欧姆定律和串联电路的电压特点,结合图甲和图乙中U1:U2=5:4列出一个电阻的比值关系式;再结合 图甲和图丙中I1:I3=2:3列出一个电阻的比值关系式,结合两个关系式便可以计算出阻值R1与R2之比.
(2)根据欧姆定律结合图乙和图丙求出两者的电流之比,再根据P=I2R计算出电阻R1的功率P1与灯L的额定功率PL之比,从而可以计算出灯L的额定功率PL.
解答:解:
S1断开,S2闭合时,电路如图甲所示;
S1和S2都断开时,电路如图乙所示;
只闭合S1时,电路如图丙所示.
(1)根据甲图和乙图可知:
∵
=
=
,
∴
=
=
;①式.
根据甲图和丙图可知:
=
=
×
=
=
,
=
;②式.
由①式和②式可解得:RL=2R2,R1=2R2,
即:
=
;RL=R1.
(2)设当开关S1和S2都断开时,电路中的电流为I2,
根据乙图和丙图可知:
=
=
=
=
,
=
=
=
=
,
则PL=
×P1=
×2W=12.5W.
答:(1)阻值R1与R2之比为2:1.
(2)灯L的额定功率PL为12.5W.
S1断开,S2闭合时,电路如图甲所示;
S1和S2都断开时,电路如图乙所示;
只闭合S1时,电路如图丙所示.

(1)根据甲图和乙图可知:
∵
| U1 |
| U2 |
| R1+R2+RL |
| R1+RL |
| 5 |
| 4 |
∴
| R2 |
| R1+ RL |
| 5-4 |
| 4 |
| 1 |
| 4 |
根据甲图和丙图可知:
| I1 |
| I3 |
| ||
|
| U |
| R1 +R2 |
| RL |
| U |
| RL |
| R1+ R2 |
| 2 |
| 3 |
| RL |
| R1+ R2 |
| 2 |
| 3 |
由①式和②式可解得:RL=2R2,R1=2R2,
即:
| R1 |
| R2 |
| 2 |
| 1 |
(2)设当开关S1和S2都断开时,电路中的电流为I2,
根据乙图和丙图可知:
| I2 |
| I3 |
| ||
|
| RL |
| R1 +R2+RL |
| 2R2 |
| 2R2+R2+2R2 |
| 2 |
| 5 |
| P1 |
| PL |
| I22R1 |
| I32RL |
| I22 |
| I32 |
| 22 |
| 52 |
| 4 |
| 25 |
则PL=
| 25 |
| 4 |
| 25 |
| 4 |
答:(1)阻值R1与R2之比为2:1.
(2)灯L的额定功率PL为12.5W.
点评:本题考查了学生对串、并联电路的判断,串联电路的特点以及欧姆定律、电功率公式的应用.本题难点在于很多同学无法将三种状态下的功率关系及电压关系联系在一起,故无法找到突破口.解答此类问题时,可将每一种情况中的已知量和未知量都找出来,仔细分析找出各情况中的关联,即可求解.

练习册系列答案
相关题目
 (2012?延庆县一模)如图所示电路,电源两端电压保持不变,闭合开关S,断开开关S1,调节滑动变阻器R2的滑片P使其接入电路的电阻值为其最大值的一半,电压表V1的示数为U1,电流表的示数为I1;闭合开关S、S1,此时小灯泡L正常发光,电流表的示数为I2;闭合开关S,断开开关S1,调节滑动变阻器R2滑片P至B端,电压表V2的示数为U2,再调节滑动变阻器R2的滑片P使接入电路的电阻值为其最大值的3/4,此时电路消耗的总功率P为1W.已知:
(2012?延庆县一模)如图所示电路,电源两端电压保持不变,闭合开关S,断开开关S1,调节滑动变阻器R2的滑片P使其接入电路的电阻值为其最大值的一半,电压表V1的示数为U1,电流表的示数为I1;闭合开关S、S1,此时小灯泡L正常发光,电流表的示数为I2;闭合开关S,断开开关S1,调节滑动变阻器R2滑片P至B端,电压表V2的示数为U2,再调节滑动变阻器R2的滑片P使接入电路的电阻值为其最大值的3/4,此时电路消耗的总功率P为1W.已知: (2012?海沧区模拟)如图所示电路,电源电压为6V.闭合开关,电阻R两端的电压为2V,电路中的电流为0.2A.求:
(2012?海沧区模拟)如图所示电路,电源电压为6V.闭合开关,电阻R两端的电压为2V,电路中的电流为0.2A.求: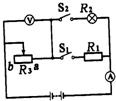 如图所示电路,电源电压保持不变,电流表的量程为0~0.6A,电表使用的是0~3V量程,定值电阻的阻值为R1=8Ω,灯泡的电阻R2=5Ω,滑动变阻器的最大阻值R3=20Ω.
如图所示电路,电源电压保持不变,电流表的量程为0~0.6A,电表使用的是0~3V量程,定值电阻的阻值为R1=8Ω,灯泡的电阻R2=5Ω,滑动变阻器的最大阻值R3=20Ω. 如图所示电路,电源电压保持不变,滑动变阻器为保护电阻,为了保证电流表、电压表及小灯泡均不被烧坏,实际操作中只允许电流表中的电流读数在O.1A~0.4A范围内变化,电压表中的电压读数在1V~2.5V之间变化.求:
如图所示电路,电源电压保持不变,滑动变阻器为保护电阻,为了保证电流表、电压表及小灯泡均不被烧坏,实际操作中只允许电流表中的电流读数在O.1A~0.4A范围内变化,电压表中的电压读数在1V~2.5V之间变化.求: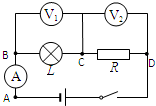 如图所示电路,电源电压保持不变,电键S闭合,电路正常工作.
如图所示电路,电源电压保持不变,电键S闭合,电路正常工作.