Question

【题目】如图所示，甲、乙是质量分布均匀的正方体物块，其密度之比ρ甲:ρ乙=1: 2。图中甲的边长为20cm，对水平面产生的压强是400Pa。求：

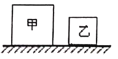
（1）图中物块甲对水平地面的压力；

（2）物块乙的密度；

（3）若甲、乙对水平地面的压强相等，现分别在两物体上沿竖直方向截去质量相等的部分并分别放在对方剩余部分的上方，若叠放后甲、乙对底面的压强增加量分别为△p甲和△p乙，且当△p甲:△p乙=5:1时，甲物体沿竖直方向截去的质量是多少kg?

Answer 1

【答案】（1）16N（2）0.4×103kg/m3 （3）0.24kg

【解析】

（1）．正方体物块甲的底面积为：

S甲=（0.2m）2=0.04m2，

根据p=，则物块甲对水平地面的压力为：

F甲=p甲S甲=400Pa×0.04m2=16N。

（2）．物块甲的重力等于其对水平地面的压力，则物块甲的重力为：

G甲=F甲=16N，

根据G=mg，物块甲的质量为：

m甲===1.6kg，

物块甲的密度为：

ρ甲===0.2×103kg/m3。

因，则物块乙的密度为；

ρ乙=2ρ甲=2×0.2×103kg/m3=0.4×103kg/m3。

（3）．若甲、乙对水平地面的压强相等，设正方体乙的边长（即高度）为h乙，因其质量分布均匀，则乙对水平地面的压强适用，所以乙的边长（即高度）为：

h乙===0.1m。

乙的重力为：

G乙=F乙=p乙S乙= p乙（h乙）2=400Pa×（0.1m）2=4N。

现分别在两物体上沿竖直方向截去质量相等的部分，设切去的质量为m，切去的体积分别为V甲′和V乙′，则甲切去的宽度为：

l甲====，

乙切去的宽度为：

l乙====。

则甲剩余部分的底面积为：

S甲′=0.2m×（0.2m- l甲）=0.2m×（0.2m-），

乙剩余部分的底面积为：

S乙′=0.1m×（0.1m- l乙）=0.1m×（0.1m-）。

将切去部分并分别放在对方剩余部分的上方，因且去的质量的相同，放到对方剩余部分上后，它们对水平地面的总压力仍然等于原来甲、乙物体的重力，则叠放后它们对地面的压强分别为：

p甲′===，

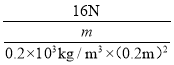p乙′===。

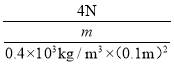则叠放后甲对底面的压强增加量为：

△p甲=400Pa- p甲′=400Pa-，

叠放后乙对底面的压强增加量为：

△p乙=400Pa- p乙′=400Pa-。

因=，即：

=，

解得m=0.24kg。即沿竖直方向切去得质量为0.24kg。

答：（1）．图中物块甲对水平地面的压力为16N；

（2）．物块乙的密度为0.4×103kg/m3；

（3）．甲物体沿竖直方向截去的质量是0.24kg。