题目内容
 火车道口处设置人工控制的栏杆,图是栏杆的示意图.密度和粗细均匀的栏杆全长6m,质量为40kg.栏杆的重心位于P点,栏杆可绕O点在竖直平面内无摩擦转动.栏杆的H端通过滑轮组来提升栏杆,其中A、B、D、E、都是定滑轮,C是动滑轮,T为固定在水平地面上的挂钩.当火车通过岔道口后,管理人员用力F1竖直向下拉绳子,栏杆恰好在水平位置平衡.管理人员为了减轻自己的工作强度,他在H端下方的绳子上加挂了一个质量为10kg的重物,用力F2以0.2m/s的速度匀速拉动绳子使栏杆逆时针转动45°角时车辆放行.此时管理人员将绳端固定在挂钩T上.已知:F1:F2=17:15;OH=1m,忽略细绳与滑轮的摩擦.g取10N/kg.求:
火车道口处设置人工控制的栏杆,图是栏杆的示意图.密度和粗细均匀的栏杆全长6m,质量为40kg.栏杆的重心位于P点,栏杆可绕O点在竖直平面内无摩擦转动.栏杆的H端通过滑轮组来提升栏杆,其中A、B、D、E、都是定滑轮,C是动滑轮,T为固定在水平地面上的挂钩.当火车通过岔道口后,管理人员用力F1竖直向下拉绳子,栏杆恰好在水平位置平衡.管理人员为了减轻自己的工作强度,他在H端下方的绳子上加挂了一个质量为10kg的重物,用力F2以0.2m/s的速度匀速拉动绳子使栏杆逆时针转动45°角时车辆放行.此时管理人员将绳端固定在挂钩T上.已知:F1:F2=17:15;OH=1m,忽略细绳与滑轮的摩擦.g取10N/kg.求:
(1)动滑轮C的重力;
(2)F1的大小;
(3)F2的功率;
(4)管理人员用力F2工作时滑轮组的效率(结果保留一位小数)
解:
(1)对杠杆进行受力分析如图1甲、乙所示:
∵OH=1m,栏杆全长6m,
∴OP=2m,
G杆=m杆g=40kg×10N/kg=400N;
G物=m物g=10kg×10N/kg=100N
当用力F1竖直向下拉绳子时,
FH1×OH=G杆×0P,
即:FH1×1m=400N×2m,
∴FH1=800N,
当用力F2匀速拉动绳子,
(FH2+G物)×OH=G杆×0P,
即:(FH2+100N)×1m=400N×2m,
∴FH2=700N;
∵忽略细绳与滑轮的摩擦,
∴F1= (FH1+G动),F2=
(FH1+G动),F2= (FH2+G动),----①
(FH2+G动),----①
∵F1:F2=17:15,
即: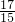 =
= =
= ,
,
解得:G动=50N,
(2)将动滑轮重代入①得:F1=425N,F2=375N,
(3)P2=F2×V=375N×0.2m/s=75W
(4)η2= =
= =
= =
= =93.3%.
=93.3%.
答:(1)动滑轮C的重力为50N;
(2)F1的大小为425N;
(3)F2的功率为75W;
(4)管理人员用力F2工作时滑轮组的效率为93.3%.
分析:(1)对杠杆进行受力分析,由于栏杆为质地均匀,重心在其中点,知道杠杆总长和OH的大小可得两边力臂大小,根据杠杆平衡条件可求当用力F1竖直向下拉绳子时、当用力F2匀速拉动绳子,杠杆左端受到的拉力;忽略细绳与滑轮的摩擦,利用F= (F拉+G动)求人的拉力,再根据F1:F2=17:15求动滑轮重;
(F拉+G动)求人的拉力,再根据F1:F2=17:15求动滑轮重;
(2)求出了动滑轮重,利用F= (F拉+G动)求人的拉力;
(F拉+G动)求人的拉力;
(3)求出了拉力F2,知道速度大小,利用P=Fv求功率大小;
(4)利用η= =
= =
= =
= 求机械效率.
求机械效率.
点评:本题考查了杠杆平衡条件的应用、使用滑轮组有用功、总功、功率、机械效率的计算,利用好杠杆平衡条件、忽略细绳与滑轮的摩擦时,F= (F拉+G动)是本题的关键.
(F拉+G动)是本题的关键.
(1)对杠杆进行受力分析如图1甲、乙所示:

∵OH=1m,栏杆全长6m,
∴OP=2m,
G杆=m杆g=40kg×10N/kg=400N;
G物=m物g=10kg×10N/kg=100N
当用力F1竖直向下拉绳子时,
FH1×OH=G杆×0P,
即:FH1×1m=400N×2m,
∴FH1=800N,
当用力F2匀速拉动绳子,
(FH2+G物)×OH=G杆×0P,
即:(FH2+100N)×1m=400N×2m,
∴FH2=700N;
∵忽略细绳与滑轮的摩擦,
∴F1=
 (FH1+G动),F2=
(FH1+G动),F2= (FH2+G动),----①
(FH2+G动),----①∵F1:F2=17:15,
即:
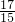 =
= =
= ,
,解得:G动=50N,
(2)将动滑轮重代入①得:F1=425N,F2=375N,
(3)P2=F2×V=375N×0.2m/s=75W
(4)η2=
 =
= =
= =
= =93.3%.
=93.3%.答:(1)动滑轮C的重力为50N;
(2)F1的大小为425N;
(3)F2的功率为75W;
(4)管理人员用力F2工作时滑轮组的效率为93.3%.
分析:(1)对杠杆进行受力分析,由于栏杆为质地均匀,重心在其中点,知道杠杆总长和OH的大小可得两边力臂大小,根据杠杆平衡条件可求当用力F1竖直向下拉绳子时、当用力F2匀速拉动绳子,杠杆左端受到的拉力;忽略细绳与滑轮的摩擦,利用F=
 (F拉+G动)求人的拉力,再根据F1:F2=17:15求动滑轮重;
(F拉+G动)求人的拉力,再根据F1:F2=17:15求动滑轮重;(2)求出了动滑轮重,利用F=
 (F拉+G动)求人的拉力;
(F拉+G动)求人的拉力;(3)求出了拉力F2,知道速度大小,利用P=Fv求功率大小;
(4)利用η=
 =
= =
= =
= 求机械效率.
求机械效率.点评:本题考查了杠杆平衡条件的应用、使用滑轮组有用功、总功、功率、机械效率的计算,利用好杠杆平衡条件、忽略细绳与滑轮的摩擦时,F=
 (F拉+G动)是本题的关键.
(F拉+G动)是本题的关键. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
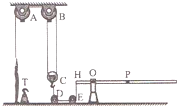 (2012?大兴区二模)火车道口处设置人工控制的栏杆,如图为栏杆的示意图.密度和粗细均匀的栏杆全长6m,质量为45kg.栏杆的重心位于P点,栏杆可绕O点在竖直平面内无摩擦转动.栏杆的H端通过滑轮组来提升栏杆,其中A、B、D、E、都是定滑轮,C是动滑轮,T为固定在水平地面上的挂钩.当火车通过岔道口后,管理人员用力F1竖直向下匀速拉绳子,使栏杆逆时针转动45°角时,管理人员将绳端固定在挂钩T上,车辆放行,在此过程中滑轮组的机械效率为η1.管理人员为了减轻自己的工作强度,他在H端下方的绳子上加挂一个质量为10kg的重物,再次进行上述操作的过程中,管理人员拉绳的力为F2,滑轮组的机械效率为η2,拉力F2,做功的功率是45W.
(2012?大兴区二模)火车道口处设置人工控制的栏杆,如图为栏杆的示意图.密度和粗细均匀的栏杆全长6m,质量为45kg.栏杆的重心位于P点,栏杆可绕O点在竖直平面内无摩擦转动.栏杆的H端通过滑轮组来提升栏杆,其中A、B、D、E、都是定滑轮,C是动滑轮,T为固定在水平地面上的挂钩.当火车通过岔道口后,管理人员用力F1竖直向下匀速拉绳子,使栏杆逆时针转动45°角时,管理人员将绳端固定在挂钩T上,车辆放行,在此过程中滑轮组的机械效率为η1.管理人员为了减轻自己的工作强度,他在H端下方的绳子上加挂一个质量为10kg的重物,再次进行上述操作的过程中,管理人员拉绳的力为F2,滑轮组的机械效率为η2,拉力F2,做功的功率是45W.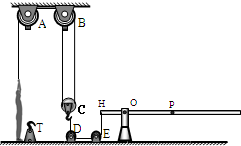 (2009?门头沟区二模)火车道口处设置人工控制的栏杆,图是栏杆的示意图.密度和粗细均匀的栏杆全长6m,质量为40kg.栏杆的重心位于P点,栏杆可绕O点在竖直平面内无摩擦转动.栏杆的H端通过滑轮组来提升栏杆,其中A、B、D、E、都是定滑轮,C是动滑轮,T为固定在水平地面上的挂钩.当火车通过岔道口后,管理人员用力F1竖直向下拉绳子,栏杆恰好在水平位置平衡.管理人员为了减轻自己的工作强度,他在H端下方的绳子上加挂了一个质量为10kg的重物,用力F2以0.2m/s的速度匀速拉动绳子使栏杆逆时针转动45°角时车辆放行.此时管理人员将绳端固定在挂钩T上.已知:F1:F2=17:15;OH=1m,忽略细绳与滑轮的摩擦.g取10N/kg.求:
(2009?门头沟区二模)火车道口处设置人工控制的栏杆,图是栏杆的示意图.密度和粗细均匀的栏杆全长6m,质量为40kg.栏杆的重心位于P点,栏杆可绕O点在竖直平面内无摩擦转动.栏杆的H端通过滑轮组来提升栏杆,其中A、B、D、E、都是定滑轮,C是动滑轮,T为固定在水平地面上的挂钩.当火车通过岔道口后,管理人员用力F1竖直向下拉绳子,栏杆恰好在水平位置平衡.管理人员为了减轻自己的工作强度,他在H端下方的绳子上加挂了一个质量为10kg的重物,用力F2以0.2m/s的速度匀速拉动绳子使栏杆逆时针转动45°角时车辆放行.此时管理人员将绳端固定在挂钩T上.已知:F1:F2=17:15;OH=1m,忽略细绳与滑轮的摩擦.g取10N/kg.求:
