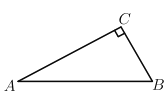
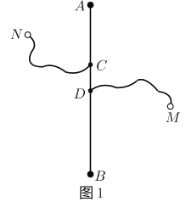
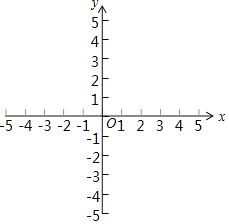【题目】如图1,长度为6千米的国道![]() 两侧有
两侧有![]() ,
,![]() 两个城镇,从城镇到公路分别有乡镇公路连接,连接点为
两个城镇,从城镇到公路分别有乡镇公路连接,连接点为![]() 和
和![]() ,其中
,其中![]() 、
、![]() 之间的距离为2千米,
之间的距离为2千米,![]() 、
、![]() 之间的距离为1千米,
之间的距离为1千米,![]() 、
、![]() 之间的乡镇公路长度为2.3千米,
之间的乡镇公路长度为2.3千米,![]() 、
、![]() 之间的乡镇公路长度为3.2千米,为了发展乡镇经济,方便两个城镇的物资输送,现需要在国道
之间的乡镇公路长度为3.2千米,为了发展乡镇经济,方便两个城镇的物资输送,现需要在国道![]() 上修建一个物流基地
上修建一个物流基地![]() ,设
,设![]() 、
、![]() 之间的距离为
之间的距离为![]() 千米,物流基地
千米,物流基地![]() 沿公路到
沿公路到![]() 、
、![]() 两个城镇的距离之和为
两个城镇的距离之和为![]() 干米,以下是对函数
干米,以下是对函数![]() 随自变量
随自变量![]() 的变化规律进行的探究,请补充完整.
的变化规律进行的探究,请补充完整.
(1)通过取点、画图、测量,得到![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| 10.5 | 8.5 | 6.5 | 10.5 | 12.5 |
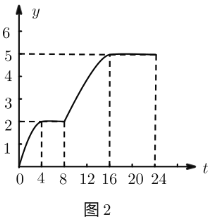
(2)如图2,建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.
(3)结合画出的函数图象,解决问题:
①若要使物流基地![]() 沿公路到
沿公路到![]() 、
、![]() 两个城镇的距离之和最小,则物流基地
两个城镇的距离之和最小,则物流基地![]() 应该修建在何处?(写出所有满足条件的位置)
应该修建在何处?(写出所有满足条件的位置)
答:__________.
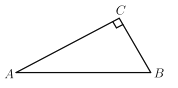
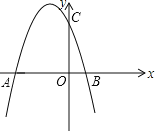
②如右图,有四个城镇![]() 、
、![]() 、
、![]() 、
、![]() 分别位于国道
分别位于国道![]() 两侧,从城镇到公路分别有乡镇公路连接,若要在国道上修建一个物流基地
两侧,从城镇到公路分别有乡镇公路连接,若要在国道上修建一个物流基地![]() ,使得
,使得![]() 沿公路到
沿公路到![]() 、
、![]() 、
、![]() 、
、![]() 的距离之和最小,则物流基地
的距离之和最小,则物流基地![]() 应该修建在何处?(写出所有满足条件的位置)
应该修建在何处?(写出所有满足条件的位置)
答:__________.

【题目】近日,某中学举办了一次以“弘扬传统文化”为主题的汉字听写比赛,初一和初二两个年级各有600名学生参加,为了更好地了解本次比赛成绩的分布情况,学校分别从两个年级随机抽取了若干名学生的成绩作为样本进行分析,下面是初二年级学生成绩样本的频数分布表和频数分布直方图(不完整,每组分数段中的分数包括最低分,不包括最高分)
初二学生样本成绩频数分布表 | ||
分组/分 | 频数 | 频率 |
50~60 | 2 | |
60~70 | 4 | 0.10 |
70~80 | 0.20 | |
80~90 | 14 | 0.35 |
90~100 | ||
合计 | 40 | 1.00 |
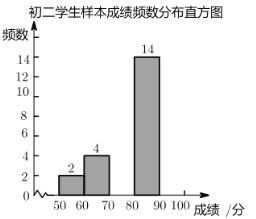
请根据所给信息,解答下列问题:
(1)补全成绩频数分布表和频数分布直方图.
(2)若初二学生成绩样本中80~90分段的具体成绩为:
80 80 81.5 82 82.5 82.5 83 84.5 85 86.5 87 88 88.5 89
①根据上述信息,估计初二学生成绩的中位数为__________.
②若初一学生样本成绩的中位数为80,甲同学在比赛中得到了82分,在他所在的年级中位居275名,根据上述信息推断甲同学所在年级为__________(选填“初一”或者“初二”).
③若成绩在85分及以上均为“优秀”,请你根据抽取的样本数据,估计初二年级学生中达到“优秀”的学生人数为__________人.
【题目】小夏同学从家到学校有![]() ,
,![]() 两条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
两条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
公交车用时 频数 公交车路线 |
|
|
|
| 总计 |
| 59 | 151 | 166 | 124 | 500 |
| 43 | 57 | 149 | 251 | 500 |
据此估计,早高峰期间,乘坐![]() 线路“用时不超过35分钟”的概率为__________,若要在40分钟之内到达学校,应尽量选择乘坐__________(填
线路“用时不超过35分钟”的概率为__________,若要在40分钟之内到达学校,应尽量选择乘坐__________(填![]() 或
或![]() )线路.
)线路.