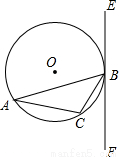
题目内容
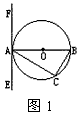
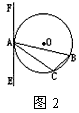
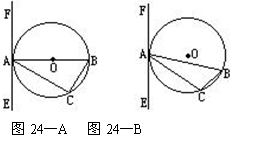
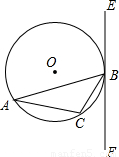
已知:△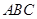 内接于⊙
内接于⊙ ,过点
,过点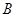 作直线
作直线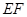 ,
, 为非直径的弦,且
为非直径的弦,且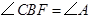 。
。

(1)求证: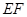 是⊙
是⊙ 的切线;
的切线;
(2)若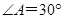 ,
,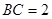 ,连结
,连结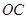 并延长交
并延长交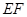 于点
于点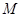 ,求由弧
,求由弧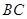 、线段
、线段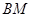 和
和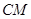 所围成的图形的面积.
所围成的图形的面积.
【答案】
(1)连结 并延长交⊙
并延长交⊙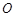 于
于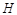 ,连结
,连结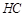 ,根据圆周角定理可得
,根据圆周角定理可得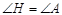 ,
, ,即得
,即得 ,再由
,再由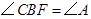 可得
可得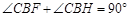 ,从而证得结论;(2)
,从而证得结论;(2) .
.
【解析】
试题分析:(1)连结 并延长交⊙
并延长交⊙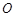 于
于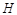 ,连结
,连结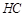 ,根据圆周角定理可得
,根据圆周角定理可得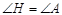 ,
, ,即得
,即得 ,再由
,再由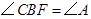 可得
可得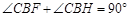 ,从而证得结论;
,从而证得结论;
(2)先根据含30°的直角三角形的性质可得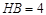 ,
,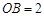 ,根据圆周角定理可得
,根据圆周角定理可得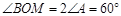 ,即可求得BM的长,最后根据
,即可求得BM的长,最后根据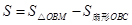 即可求得结果.
即可求得结果.
(1)连结 并延长交⊙
并延长交⊙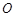 于
于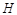 ,连结
,连结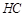 ,
,
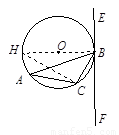
则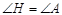
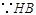 是直径,
是直径,
∴
∴ .
.
又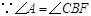
∴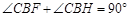
∴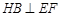 .
.
又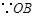 是半径,
是半径,
∴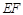 是⊙
是⊙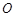 的切线.
的切线.
(2)在Rt△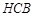 中,
中,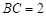 ,
,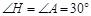 ,
,

∴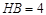 ,
,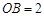 .
.
∵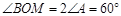 ,
,
∴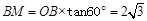 ,
,
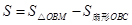
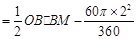
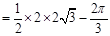
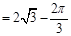 .
.
∴由弧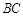 、线段
、线段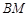 和
和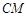 所围成的图形的面积为
所围成的图形的面积为 .
.
考点:圆周角定理,切线的判定,含30°的直角三角形的性质,三角形的面积公式,扇形的面积公式
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
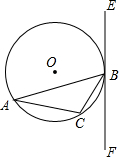 已知:△ABC内接于⊙O,过点B作直线EF,AB为非直径的弦,且∠CBF=∠A.
已知:△ABC内接于⊙O,过点B作直线EF,AB为非直径的弦,且∠CBF=∠A.