题目内容
如图,正方形EFGH的顶点在边长为a的正方形ABCD的边上,若AE=x,正方形EFGH的面积为y.
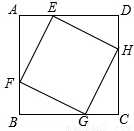
(1)求出y与x之间的函数关系式;
(2)正方形EFGH有没有最大面积?若有,试确定E点位置;若没有,说明理由.
【答案】
(1)y=2x2-2ax+a2 (2) 有.当点E是AB的中点时,面积最大.
【解析】本题考查了二次函数的应用.
(1)先由AAS证明△AEF≌△DHE,得出AE=DH=x米,AF=DE=(a-x)米,再根据勾股定理,求出EF2,即可得到S与x之间的函数关系式;
(2)先将(1)中求得的函数关系式运用配方法写成顶点式,再根据二次函数的性质即可求解.
解:∵四边形ABCD是边长为a米的正方形,
∴∠A=∠D=90°,AD= a米.
∵四边形EFGH为正方形,
∴∠FEH=90°,EF=EH.
在△AEF与△DHE中,
∵∠A=∠D,∠AEF=∠DHE=90°-∠DEH,EF=EH
∴△AEF≌△DHE(AAS),
∴AE=DH=x米,AF=DE=(a-x)米,
∴y=EF2=AE2+AF2=x2+(a-x)2=2x2-2ax+ a2,
即y=2x2-2ax+ a2;
(2)∵y=2x2-2ax+ a2=2(x- )2+
)2+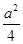 ,
,
∴当x= 时,S有最大值.
时,S有最大值.
故当点E是AB的中点时,面积最大.

练习册系列答案
相关题目
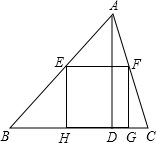 如图,正方形EFGH内接于△ABC,设BC=
如图,正方形EFGH内接于△ABC,设BC=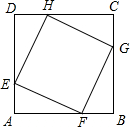 如图,正方形EFGH的四个顶点在正方形ABCD的边上,若AB=a,EF=b,则△AEF的内切圆半径为
如图,正方形EFGH的四个顶点在正方形ABCD的边上,若AB=a,EF=b,则△AEF的内切圆半径为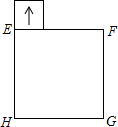 如图,正方形EFGH的边长是3cm,一个边长为1cm的小正方形沿着正方形EFGH的边EF→FG→GH→HE连续地翻转,那么这个小正方形回到起始位置时,它的方向是下图的( )
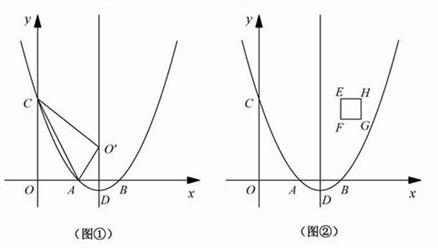
如图,正方形EFGH的边长是3cm,一个边长为1cm的小正方形沿着正方形EFGH的边EF→FG→GH→HE连续地翻转,那么这个小正方形回到起始位置时,它的方向是下图的( )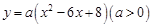 的图象与x轴分别交于点A、B,与y轴交于点C.点D是抛物线的顶点.
的图象与x轴分别交于点A、B,与y轴交于点C.点D是抛物线的顶点.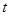 个单位长度时,正方形EFGH上是否存在一点P(包括正方形的边界),使得四条线段PA、PB、PC、PD能够构成平行四边形?如果存在,请求出
个单位长度时,正方形EFGH上是否存在一点P(包括正方形的边界),使得四条线段PA、PB、PC、PD能够构成平行四边形?如果存在,请求出