题目内容
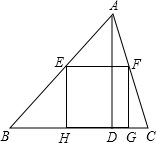 如图,正方形EFGH内接于△ABC,设BC=
如图,正方形EFGH内接于△ABC,设BC=. |
| ab |
. |
| ab |
分析:由题意可知:a、b、c、d为连续四个整数故可设为a,a+1,a+2,a+3,其中BC=11a+1,(1≤a≤8的正整数),易证△AEF∽△ABC,可得:
=
解得a=1或a=5,可求得△ABC的面积为24或224.
| a+2 |
| 11a+1 |
| 1 |
| a+3 |
解答:解:a、b、c、d为连续四个整数故可设为a,a+1,a+2,a+3,
∵BC=
,
∴BC=11a+1,
∵四边形EFGH是正方形,
∴EF∥BC,
∴△AEF∽△ABC,
∴
=
,
即
=
,
解关于a的方程,得
a1=1,a2=5,
∴S△ABC=
BC×AD=24,或S△ABC=
BC×AD=224.
∵BC=
. |
| ab |
∴BC=11a+1,
∵四边形EFGH是正方形,
∴EF∥BC,
∴△AEF∽△ABC,
∴
| EF |
| BC |
| AD-EH |
| AD |
即
| a+2 |
| 11a+1 |
| 1 |
| a+3 |
解关于a的方程,得
a1=1,a2=5,
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了相似三角形的判定和性质、三角形面积公式、平行线分线段成比例定理的推论、解一元二次方程、相似三角形高的比等于相似比.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
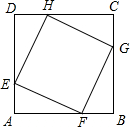 如图,正方形EFGH的四个顶点在正方形ABCD的边上,若AB=a,EF=b,则△AEF的内切圆半径为
如图,正方形EFGH的四个顶点在正方形ABCD的边上,若AB=a,EF=b,则△AEF的内切圆半径为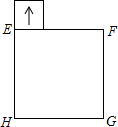 如图,正方形EFGH的边长是3cm,一个边长为1cm的小正方形沿着正方形EFGH的边EF→FG→GH→HE连续地翻转,那么这个小正方形回到起始位置时,它的方向是下图的( )
如图,正方形EFGH的边长是3cm,一个边长为1cm的小正方形沿着正方形EFGH的边EF→FG→GH→HE连续地翻转,那么这个小正方形回到起始位置时,它的方向是下图的( )
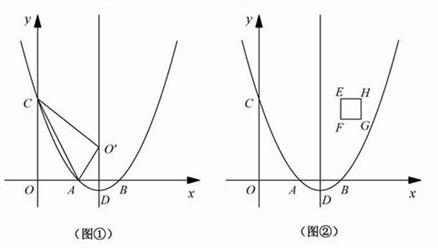
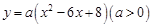 的图象与x轴分别交于点A、B,与y轴交于点C.点D是抛物线的顶点.
的图象与x轴分别交于点A、B,与y轴交于点C.点D是抛物线的顶点.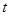 个单位长度时,正方形EFGH上是否存在一点P(包括正方形的边界),使得四条线段PA、PB、PC、PD能够构成平行四边形?如果存在,请求出
个单位长度时,正方形EFGH上是否存在一点P(包括正方形的边界),使得四条线段PA、PB、PC、PD能够构成平行四边形?如果存在,请求出