题目内容
已知二次函数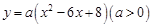 的图象与x轴分别交于点A、B,与y轴交于点C.点D是抛物线的顶点.
的图象与x轴分别交于点A、B,与y轴交于点C.点D是抛物线的顶点.
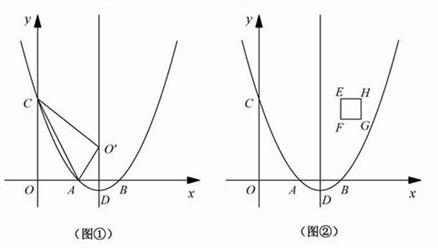
(1)如图①,连接AC,将△OAC沿直线AC翻折,若点O的对应点O'恰好落在该抛物线的对称轴上,求实数a的值;
(2)如图②,在正方形EFGH中,点E、F的坐标分别是(4,4)、(4,3),边HG位于边EF的右侧.若点P是边EF或边FG上的任意一点,求证四条线段PA、PB、PC、PD不能构成平行四边形;
(3)如图②,正方形EFGH向左平移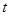 个单位长度时,正方形EFGH上是否存在一点P(包括正方形的边界),使得四条线段PA、PB、PC、PD能够构成平行四边形?如果存在,请求出
个单位长度时,正方形EFGH上是否存在一点P(包括正方形的边界),使得四条线段PA、PB、PC、PD能够构成平行四边形?如果存在,请求出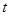 的取值范围.
的取值范围.
(1)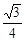 (2)不能构成平行四边形。理由见解析(3)
(2)不能构成平行四边形。理由见解析(3)
【解析】解:(1)令y=0,由a(x2-6x+8)=0解得x1=2,x2=4;
令x=0,解得y=8a
∴点A、B、C的坐标分别是(2,0)、(4,0)、(0,8a),该抛物线对称轴为直线x=3
∴OA=2
如图①设抛物线对称轴与x轴的交点为M,则AM=1
由题意得 =OA=2
=OA=2
∴ =2AM,∴∠
=2AM,∴∠ =60°
=60°
∴∠OAC=∠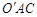 =60°
=60°
∴OC= ·AO=2
·AO=2 ,即8a=2
,即8a=2 ,∴a=
,∴a=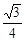 .
…………………………(3分)
.
…………………………(3分)
(2)若点P是边EF或边FG上的任意一点,结果同样成立.
(I)如图②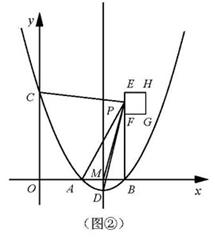
设P是边EF上的任意一点(不与点E重合),连接PM.
∵点E(4,4)、F(4,3)与点B(4,0)在一直线上,点C在y轴上,
∴PB<4,PC≥4,∴PC>PB.
又PD>PM>PB,PA>PM>PB,
∴PB≠PA,PB≠PC,PB≠PD,
∴此时线段PA、PB、PC、PD不能构成平行四边形. …………………………(3分)
(II)设P是边FG上的任意一点(不与点G重合),
点F的坐标是(4,3)点G的坐标是(5,3).
∴FB=3,GB=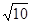 ,∴3≤PB<
,∴3≤PB<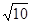 ,
,
∵PC≥4,∴PC>PB
又PD>PM>PB,PA>PM>PB,
∴PB≠PA,PB≠PC,PB≠PD,
∴此时线段PA、PB、PC、PD不能构成平行四边形. …………………………(3分)
(3)
(1)令y=0,解得x1=2,x2=4,令x=0,解得y=8a,得出点A、B、C的坐标,求得该抛物线对称轴为直线x=3,再根据∠OAC==60°得出AO ,从而求出a
(2)分两种情况进行讨论,一种设P是边EF上的任意一点(不与点E重合)可得PC>PB. 从而得出PB≠PA,PB≠PC,PB≠PD,即可求出线段PA、PB、PC、PD不能构成平行四边形;同理,另一种设P是边FG上的任意一点(不与点G重合),也可求出线段PA、PB、PC、PD不能构成平行四边形;
(3)先求出PA=PB,再由PC=PD,列出关于t与a的方程,从而求出a的值,即可求出答案

A、y=
| ||
B、y=-
| ||
C、y=-
| ||
D、y=
|
 已知二次函数的图象与x轴交于点A(-1,0)和点B(3,0),且与直线y=kx-4交y轴于点C.
已知二次函数的图象与x轴交于点A(-1,0)和点B(3,0),且与直线y=kx-4交y轴于点C.