题目内容
【题目】如图,已知抛物线y=ax2+bx+3交x轴于A、B两点(A在B左边),交y轴于C点,且OC=3OA,对称轴x=1交抛物线于D点.
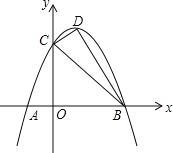
(1)求抛物线解析式;
(2)在直线BC上方的抛物线上找点E使S△BCD=S△BCE,求E点的坐标;
(3)在x轴上方的抛物线上,是否存在点M,过M作MN⊥x轴于N点,使△BMN与△BCD相似?若存在,请求出M的坐标;若不存在,请说明理由.
【答案】(1)y=﹣x2+2x+3.(2)E(2,3).(3)存在,存在点M(2,3)或(﹣![]() ,
,![]() ),使△BMN与△BCD相似.
),使△BMN与△BCD相似.
【解析】
试题分析:(1)将x=0代入可求得y=3,故此可知C(0,3),OC=3,OA=1,则点A的坐标为(﹣1,0),由点B与点A关于x=1对称可知B(3,0),将点A、点B的坐标代入抛物线的解析式,从而可求得a=﹣1,b=2;
(2)过D点作DE∥BC交抛物线y=﹣x2+2x+3于E点,由△BCD与△BCE是同底等高的三角形可知S△BCD=S△BCE,设直线DE的解析式为y=﹣x+b,将点D的坐标代入可求得直线DE的解析式,然后与抛物线的解析式联立可求得点E的坐标;
(3)由两点间的而距离公式可知:BC=3![]() ,CD=
,CD=![]() ,设M(x,y),则MN=y=﹣x2+2x+3,BN=3﹣x,然后根据相似三角形的性质列出关于x的方程,从而可求得点M的坐标.
,设M(x,y),则MN=y=﹣x2+2x+3,BN=3﹣x,然后根据相似三角形的性质列出关于x的方程,从而可求得点M的坐标.
解:(1)∵将x=0代入得y=3,
∴C(0,3).
∵OC=3OA,
∴OA=1.
∴A(﹣1,0).
∵点B与点A关于x=1对称,
∴B(3,0).
将A(﹣1,0),B(3,0)代入y=ax2+bx+3得:![]() ,
,
解得:![]() .
.
∴抛物线解析式为y=﹣x2+2x+3.
(2)∵将x=1代入抛物线的解析式得:y=﹣1+2+3=4,
∴D(1,4).
如图1,过D点作DE∥BC交抛物线y=﹣x2+2x+3于E点.
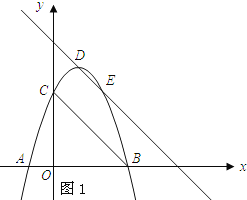
设直线DE的解析式为y=﹣x+b,
将点D的坐标代入得:﹣1+b=4,解得:b=5,则直线DE的解析式为y=﹣x+5.
将y=﹣x+5与y=﹣x2+2x+3联立得:![]() ,
,
解得:![]() (舍去),
(舍去),![]() .
.
∴E(2,3).
(3)存在.
由两点间的而距离公式可知:BC=![]() 3
3![]() ,CD=
,CD=![]() =
=![]() .
.
设M(x,y),则MN=y=﹣x2+2x+3,BN=3﹣x.
①如图2所示:

∵当△BMN∽△DBC时,![]() ,
,
∴![]() .
.
解得:x1=2,x2=3(舍去).
∵当x=2时,y=3,
∴M(2,3).
②如图3所示:
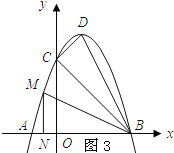
∵当△BMN∽△BDC时,![]() ,
,
∴![]() .
.
解得:x1=﹣![]() ,x2=3(舍去).
,x2=3(舍去).
当x=﹣![]() 时,y=
时,y=![]() ,
,
∴M(﹣![]() ,
,![]() )
)
综上,存在点M(2,3)或(﹣![]() ,
,![]() ),使△BMN与△BCD相似.
),使△BMN与△BCD相似.

 备战中考寒假系列答案
备战中考寒假系列答案