Question

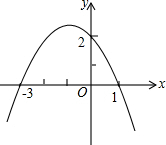抛物线y=ax²+bx+c（a＜0）如图所示，则下列说法正确的是（　　）

A．c=0

B．当x＞-1时y随x的增大而增大

C．图象的对称轴是直线x=-2

D．不等式ax²+bx+c＞0的解集是-3＜x＜1

Answer 1

分析：根据抛物线与y轴的交点在x轴上方可对A进行判断；先利用抛物线与x轴的交点坐标可得到抛物线的对称轴为直线x=-1，再根据抛物线的增减性即可对B、C进行判断；观察函数图象得到当-3＜x＜1时，y＞0，即ax²+bx+c＞0，于是可对D进行判断．

解答：解：A、抛物线与y轴的交点在x轴上方，则c＞0，所以A选项错误；
B、因为抛物线过（-3，0），（1，0），则抛物线的对称轴为直线x=-1，而抛物线开口向下，所以当x＞-1时y随x的增大而减小，所以B选项错误；
C、抛物线的对称轴为直线x=-1，所以C选项错误；
D、当-3＜x＜1时，y＞0，即ax²+bx+c＞0，所以D选项正确．
故选D．

点评：本题考查了二次函数的图象与系数的关系：二次函数y=ax²+bx+c（a≠0）的图象为抛物线，当a＞0，抛物线开口向上；对称轴为直线x=-

b

2a

；抛物线与y轴的交点坐标为（0，c）；当b²-4ac＞0，抛物线与x轴有两个交点；当b²-4ac=0，抛物线与x轴有一个交点；当b²-4ac＜0，抛物线与x轴没有交点．