题目内容
Rt△ABC中，∠BAC=90°，AB=AC，D是BC的中点，AE=BF。
求证：△DEF为等腰直角三角形
求证：△DEF为等腰直角三角形
证明：（1）连接AD，
∵Rt△ABC中，∠BAC=90°，AB=AC，
∴∠B=∠C=45°
∵AB=AC，DB=BC
∴∠DAE=∠BAD=45°
∴∠BAD=∠B=45°
∴AD=BD，∠ADB=90°
∵AE=BF，∠DAE=∠B=45°，AD=BD
∴△DAE≌△DBF（SAS）
∴DE=DF，∠ADE=∠BDF
∵∠BDF+∠ADF=∠ADB=90°
∴∠ADE+∠ADF=90°
∴△DEF为等腰直角三角形。
∵Rt△ABC中，∠BAC=90°，AB=AC，
∴∠B=∠C=45°
∵AB=AC，DB=BC
∴∠DAE=∠BAD=45°
∴∠BAD=∠B=45°
∴AD=BD，∠ADB=90°
∵AE=BF，∠DAE=∠B=45°，AD=BD
∴△DAE≌△DBF（SAS）
∴DE=DF，∠ADE=∠BDF
∵∠BDF+∠ADF=∠ADB=90°
∴∠ADE+∠ADF=90°
∴△DEF为等腰直角三角形。
练习册系列答案
冲刺100分1号卷系列答案
期末好成绩系列答案
相关题目
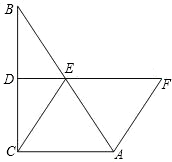延长线上，且AF=CE．求证：四边形ACEF是菱形．
如图，在Rt△ABC中，∠BAC=90°，点D、E、F分别是三边的中点，且CF=3cm，则DE=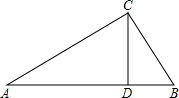
如图，Rt△ABC中，AC⊥BC，CD⊥AB于D，AC=8，BC=6，则AD=
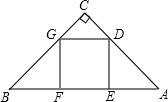点G在边BC上．
如图，Rt△ABC中，∠C=90°，D为AB的中点，DE⊥AB，AB=20，AC=12，则四边形ADEC的面积为