题目内容
【题目】如图1,已知MN∥PQ,B在MN上,C在PQ上,A在B的左侧,D在C的右侧,DE平分∠ADC,BE平分∠ABC,直线DE、BE交于点E,∠CBN=100°.
(1)若∠ADQ=130°,求∠BED的度数;
(2)将线段AD沿DC方向平移,使得点D在点C的左侧,其他条件不变,若∠ADQ=n°,求∠BED的度数(用含n的代数式表示).
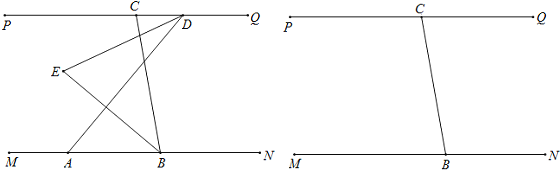
【答案】(1)∠BED=65°;(2)∠BED=220°﹣![]() n°.
n°.
【解析】试题分析:(1)过点E作EF∥PQ,由平行线的性质及角平分线求得∠DEF和∠FEB,即可求出∠BED的度数;
(2)过点E作EF∥PQ,由平行线的性质及角平分线求得∠DEF和∠FEB,即可求出∠BED的度数;
试题解析:
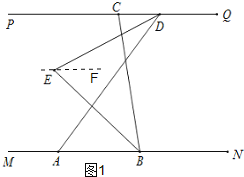
(1)如图1,过点E作EF∥PQ,
∵∠CBN=100°,∠ADQ=130°,
∴∠CBM=80°,∠ADP=50°,
∵DE平分∠ADC,BE平分∠ABC,
∴∠EBM=![]() ∠CBM=40°,
∠CBM=40°,
∠EDP=![]() ∠ADP=25°,
∠ADP=25°,
∵EF∥PQ,
∴∠DEF=∠EDP=25°,
∵EF∥PQ,MN∥PQ,
∴EF∥MN.
∴∠FEB=∠EBM=40°
∴∠BED=25°+40°=65°;
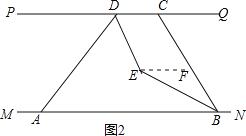
(2)如图2,过点E作EF∥PQ,
∵∠CBN=100°,
∴∠CBM=80°,
∵DE平分∠ADC,BE平分∠ABC,
∴∠EBM=![]() ∠CBM=40°,∠EDQ=
∠CBM=40°,∠EDQ=![]() ∠ADQ=
∠ADQ=![]() n°,
n°,
∵EF∥PQ,
∴∠DEF=180°﹣∠EDQ=180°﹣![]() n°,
n°,
∵EF∥PQ,MN∥PQ,
∴EF∥MN,
∴∠FEB=∠EBM=40°,
∴∠BED=180°﹣![]() n°+40°=220°﹣
n°+40°=220°﹣![]() n°.
n°.

练习册系列答案
相关题目