Question

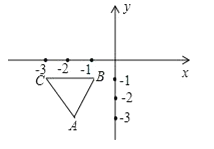
【题目】如图，抛物线y=-x2+bx+c与x轴交于A(1，0)，B(-3，0)两点，与y轴交于点C.

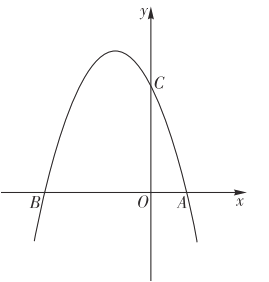
（1）求该抛物线的解析式；

（2）设该抛物线的顶点为D，求出△BCD的面积.

Answer 1

【答案】（1） ；（2）3

【解析】

（1）利用待定系数法把两已知点代入即可求；（2）求出顶点D坐标后连接BD，CD，BC用中垂高与水平宽乘积一半的面积公式计算即可.

解:(1)把点A(1,0),B(-3,0)代入y=-x2+bx+c中,得 ,

解得

∴抛物线的解析式为

(2)如图，连接BD,CD,BC,过点D作DE⊥x轴,交BC于点E.

∵,

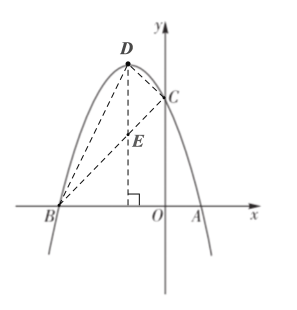
∴D(- 1,4),C(0,3).

∵B(-3,0),

∴直线BC的解析式为y=x +3,OB=3.

当x=-1时,y=-1+3=2.

∴E(- 1 ,2).

∴DE =2.

∴S△BCD =S△BED十S△DEC

=

=

=3