��Ŀ����
����Ŀ���Ķ����н����̣���ͼ�ף�AB��CD��̽����P���A����C֮��Ĺ�ϵ��
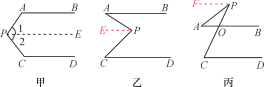
�⣺����P��PE��AB.
��AB��CD��
��PE��AB��CD(ƽ����ͬһ��ֱ�ߵ�����ֱ����ƽ��)��
���1����A��180��(��ֱ��ƽ�У�ͬ���ڽǻ���)��
��2����C��180��(��ֱ��ƽ�У�ͬ���ڽǻ���)��
���1����A����2����C��360��.
�֡ߡ�APC����1����2��
���APC����A����C��360��.
��ͼ�Һ�ͼ����AB��CD����������������ֱ�̽����ͼ�С�P���A����C֮��Ĺ�ϵ��
���𰸡�ͼ�ң���APC����A����C��ͼ������C����A����APC.
��������
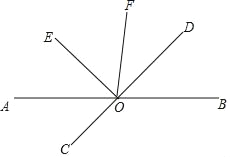
ͼ���У���P��PE��AB.��AB��CD��PE�����������ڴ������ת����֮��Ĺ�ϵ��ͼ���У�����P��PF��AB. ���������ڴ������ת����֮��Ĺ�ϵ.
�⣺��ͼ�ң�����P��PE��AB.
��AB��CD(��֪)��
��PE��AB��CD(ƽ����ͬһֱ�ߵ�����ֱ��ƽ��)��
���A����EPA����EPC����C(��ֱ��ƽ�У��ڴ������)��
�ߡ�APC����EPA����EPC��
���APC����A����C(��������)��
��ͼ��������P��PF��AB.
���FPA����A(��ֱ��ƽ�У��ڴ������)��
��AB��CD(��֪)��
��PF��CD(ƽ����ͬһֱ�ߵ�����ֱ��ƽ��)��
���FPC����C(��ֱ��ƽ�У��ڴ������)��
�ߡ�FPC����FPA����APC��
���C����A����APC(��������)��

����Ŀ��Ϊ�����ѧ����д���ֵ���������ǿ�������ֵ���ʶ�������ٰ��ˡ�������д����������ѡ�κ���50��ѧ���μӾ�������50��ѧ��ͬʱ��д50�����֣���ÿ��ȷ��д��һ�����ֵ�1�֣����ݲ��Գɼ����Ƴ�����Ƶ���ֲ����Ͳ���Ƶ���ֲ�ֱ��ͼ��ͼ����
��� | �ɼ�x�� | Ƶ���������� |
��1�� | 25��x��30 | 4 |
��2�� | 30��x��35 | 6 |
��3�� | 35��x��40 | 14 |
��4�� | 40��x��45 | a |
��5�� | 45��x��50 | 10 |
����ͼ��������и��⣺
��1�������a��ֵ��
��2�����Ƶ���ֲ�ֱ��ͼ����������
��3�������Գɼ�������40��Ϊ���㣬�β��Ե��������Ƕ��٣�