��Ŀ����
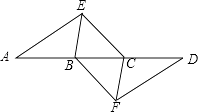
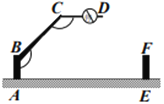
����Ŀ��ƽ���ı��ο��Կ������߶�ƽ�Ƶõ���ͼ�Σ���ͼ1�����߶�AD��AB�ķ���ƽ��AB����λ��BC�����Ϳ��Եõ�ƽ���ı���ABCD�����߽��߶�AB��AD�ķ���ƽ��AD����λ��DC����Ҳ���Եõ�ƽ���ı���ABCD��
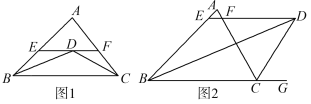
��1����ͼ2��ͼ3��ͼ4�У�����ƽ���ı���ABCD�Ķ���A��B��D�����꣬д��ͼ2��ͼ3��ͼ4�еĶ���C�����꣬���Ƿֱ���_____��_______��_______��
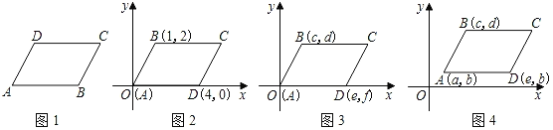
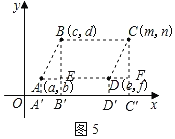
��2��ͨ����ͼ2��3��4�Ĺ۲�Ͷ���C�������̽������ᷢ�֣�����ƽ���ı���ABCD����ֱ������ϵ���ĸ�λ�ã����䶥������ΪA��a��b����B��c��d����C��m��n����D��e��f������ͼ5��ʱ�����ĸ�����ĺ�����a��c��m��e֮��ĵ�����ϵΪ______��������b��d��n��f֮��ĵ�����ϵΪ_______������֤������
��3����ͼ6����ƽ��ֱ������ϵ�У���֪A����3��0����B��3��0����C��2��4��������A��B��C������Ϊ�����ƽ���ı��εĵ��ĸ�����D������Ϊ______��
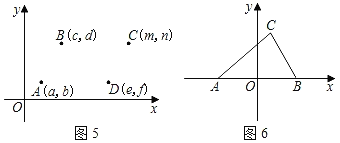
���𰸡���1����5��2������e+c��d������c+e��a��d������2��m��c+e��a��n��d+f��b����3����8��4����2����4����4��4����
��������
��1������ƽ���ı��ε����ʣ��Ա�ƽ������ȣ���⼴�ɣ�
��2����ͼ�������ߣ�֤����BEA�ա�CFD��AAS�����Ƴ�AE��DF��c��a��BE��CF��d��b������֪C�������Ϊ��m��n�����ɵ�m��e��c��a��n��d��b��f��
��3���ɣ�2���Ľ��ۼ��ɵó��𰸣�
�⣺��1����ƽ���ı��ε����ʺ�ƽ�Ƶ����ʵã�ͼ1��ͼ2��3�ж���C������ֱ��ǣ���5��2������e+c��d������c+e��a��d����
�ʴ�Ϊ����5��2������e+c��d������c+e��a��d����
��2���ֱ����A��B��C��D��x��Ĵ��ߣ�����ֱ�ΪA'��B'��C'��D'��
�ֱ��A��D��AE��BB'��E��DF��CC'�ڵ�F��
��ƽ���ı���ABCD�У�CD��BA��CD��BA��
��![]() ��
��
����BEA����CFD��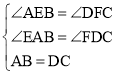 ��
��
���BEA�ա�CFD��AAS����
��AE��DF��c��a��BE��CF��d��b��
��C���������m��n����
��m��e��c��a��n��d��b��f����m��c+e��a��n��d+f��b
�ʴ�Ϊ��m��c+e��a��n��d+f��b��
��3�����ı���ABCD��ƽ���ı��Σ�A����3��0����B��3��0����C��2��4����
�ɣ�2���ã�m��c+e��a��n��d+f��b��
���D��������3+2+3��0+4��0����3+3��2��0+0��4����3+2��3��0+4-0����
����D������8��4����2����4����4��4����
�ʴ�Ϊ����8��4����2����4����4��4����

����Ŀ��ij������һ�ֹ��ߣ����г����飬����ÿ������280Ԫ����ʱ��ÿ�¿�����300���������۵���ÿ����1Ԫ��ÿ�¿ɶ��۳�2������ͳ�ƣ�ÿ�����ߵĹ̶��ɱ�Q��Ԫ����������y�������������¹�ϵ��
������y������ | 100 | 160 | 240 | 320 |
ÿ�����ߵĹ̶��ɱ�Q��Ԫ�� | 96 | 60 | 40 | 30 |
��1��д���²�����y�����������۵���x��Ԫ��֮��ĺ�����ϵʽ��
��2����ÿ����ߵĹ̶��ɱ�Q��Ԫ�����²�����y������֮��ĺ�����ϵʽ��
��3�����ó�������ߵ��²�����������400������ÿ����ߵĹ̶��ɱ�����Ϊ����Ԫ�����۵������Ϊ����Ԫ��