题目内容
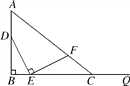
【题目】如图，AB＝4，射线BQ和AB互相垂直，点D是AB上的一个动点，点E在射线BQ上，BE＝
DB，作EF⊥DE，并截取EF＝DE，连接AF并延长交射线BQ于点C.设BE＝x，BC＝y，则y关于x的函数解析式为______________．
【答案】y＝
(0＜x≤2)
【解析】作FM⊥BC于M．
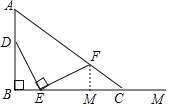
∵∠DBE=∠DEF=∠EMF=90°，
∴∠DEB+∠BDE=90°，∠DEB+∠FEM=90°，
∴∠BDE=∠FEM．
在△DBE和△EMF中，
∠BDE=∠FEM，
∠B=∠EMF，
DE=EF，
∴△DBE≌△EMF，
∴FM=BE=x，EM=BD=2BE=2x，
∵FM∥AB，
∴FM:AB=CM:CB，
∴x:4=(y3x):y，
∴y＝
（0＜x≤2）．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
