题目内容
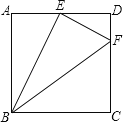
【题目】在正方形ABCD中,点E为AD中点,DF=![]() CD,则下列说法:(1)BE⊥EF;(2)图中有3对相似三角形;(3)E到BF的距离为
CD,则下列说法:(1)BE⊥EF;(2)图中有3对相似三角形;(3)E到BF的距离为![]() AB;(4)
AB;(4)![]() =
=![]() .其中正确的有( )
.其中正确的有( )
A.4个 B.3个 C.2个 D.1个
【答案】B
【解析】
试题分析:根据正方形的性质得到AD=AB=BC=CD,∠A=∠ABC=C=∠D=90°,由于点E为AD中点,DF=![]() CD,于是得到
CD,于是得到![]() =2,推出△ABE∽△DEF,根据相似三角形的性质得到∠ABE=∠DEF,根据平角的定义得到∠BEF=90°,于是求得BE⊥EF;故①正确;根据相似三角形的性质得到
=2,推出△ABE∽△DEF,根据相似三角形的性质得到∠ABE=∠DEF,根据平角的定义得到∠BEF=90°,于是求得BE⊥EF;故①正确;根据相似三角形的性质得到![]() ,等量代换得到
,等量代换得到![]() ,推出△ABE∽△BEF,于是得到△ABE∽△BEF∽△DEF,即可得到图中有3对相似三角形;故②正确;根据相似三角形的性质得到∠ABE=∠EBF,根据角平分线的性质得到E到BF的距离=AE,于是得到E到BF的距离为
,推出△ABE∽△BEF,于是得到△ABE∽△BEF∽△DEF,即可得到图中有3对相似三角形;故②正确;根据相似三角形的性质得到∠ABE=∠EBF,根据角平分线的性质得到E到BF的距离=AE,于是得到E到BF的距离为![]() AB;故③正确;设DF=1,则AE=DE=2,AB=BC=CD=4,由勾股定理得到BE=
AB;故③正确;设DF=1,则AE=DE=2,AB=BC=CD=4,由勾股定理得到BE=![]() =2
=2![]() ,EF=
,EF=![]() =
=![]() ,求得S△BEF=
,求得S△BEF=![]() BEEF=5,S△BCF=
BEEF=5,S△BCF=![]() BCCF=
BCCF=![]() =6于是得到
=6于是得到![]() =
=![]() ,故④错误.
,故④错误.
解:在正方形ABCD中,
∵AD=AB=BC=CD,∠A=∠ABC=C=∠D=90°,
∵点E为AD中点,DF=![]() CD,
CD,
∴![]() =2,
=2,
∴△ABE∽△DEF,
∴∠ABE=∠DEF,
∵∠AEB+∠ABE=90°,
∴∠AEB+∠DEF=90°,
∴∠BEF=90°,
∴BE⊥EF;故①正确;
∵△ABE∽△DEF,
∴![]() ,
,
∴![]() ,
,
∵∠A=∠BEF=90°,
∴△ABE∽△BEF,
∴△ABE∽△BEF∽△DEF,
∴图中有3对相似三角形;故②正确;
∵△ABE∽△BEF,
∴∠ABE=∠EBF,
∴E到BF的距离=AE,
∴E到BF的距离为![]()
设DF=1,则AE=DE=2,AB=BC=CD=4,
∴CF=3,
∴BE=![]() =2
=2![]() ,EF=
,EF=![]() =
=![]() ,
,
∴S△BEF=![]() BEEF=5,S△BCF=
BEEF=5,S△BCF=![]() BCCF=
BCCF=![]() =6
=6
∴![]() =
=![]() ,故④错误,
,故④错误,
故选B.


