题目内容
【题目】如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为( )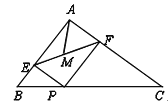
A.2
B.2.4
C.2.6
D.3
【答案】B
【解析】先求证四边形AFPE是矩形,再根据直线外一点到直线上任一点的距离,垂线段最短,利用相似三角形对应边成比例即可求得AP最短时的长,然后即可求出AM最短时的长.
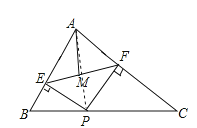
连结AP,在△ABC中,AB=6,AC=8,BC=10,
∴∠BAC=90°,
∵PE⊥AB,PF⊥AC,
∴四边形AFPE是矩形,
∴EF=AP.
∵M是EF的中点,
∴AM=![]() AP,
AP,
根据直线外一点到直线上任一点的距离,垂线段最短,
即AP⊥BC时,AP最短,同样AM也最短,
∴当AP⊥BC时,△ABP∽△CBA,
∴![]() ,
,
∴![]() ,
,
∴AP最短时,AP=4.8
∴当AM最短时,AM=![]() =2.4.
=2.4.
故选B.
【考点精析】根据题目的已知条件,利用垂线段最短和直角三角形斜边上的中线的相关知识可以得到问题的答案,需要掌握连接直线外一点与直线上各点的所有线段中,垂线段最短;现实生活中开沟引水,牵牛喝水都是“垂线段最短”性质的应用;直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
相关题目