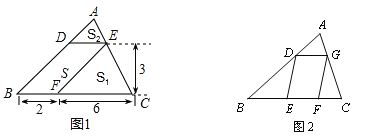��Ŀ����
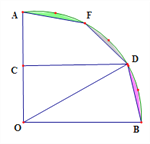
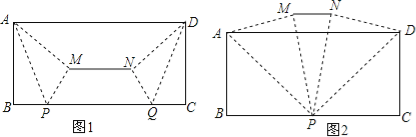
����Ŀ����������⣩��ͼ1��С����һ��ADΪ12����ABΪ4�ij�����ֽƬ�����·�ʽ�����۵�����ֽƬ��һ��BC�Ϸֱ�ȡ��P��Q��ʹ��BP=CQ������AP��DQ������ABP����DCQ�ֱ���AP��DQ�۵�����APM����DQN������MN��С�������߶�MN��λ�úͳ������ŵ�P��Q��λ�÷����ı䣮
������̽����
��1������ͼ1�й���M��N�ֱ�ME��BC�ڵ�E��NF��BC�ڵ�F��
��֤����ME=NF����MN��BC��
��������⣩
��2����ͼ1����BP=3�����߶�MN�ij���
��3����ͼ2������P���Q�غ�ʱ����MN�ij���
���𰸡���1����֤�������������֤�������������2��![]() ����3��
����3��![]() ��
��
��������
���⣨1�����Ȱ���Ҫ����ͼ��֤���߶���ȣ�ͨ��֤�����ڵ�������ȫ�ȣ�����֤��ME=NF��Ҫ֤����MEP�ա�NPQ����֤����ABP�ա�DCQ������APB=��DQG��Ȼ��֤����MEP�ա�NPQ��AAS������֤�ý��ۣ���ֻҪ֤��MN��EF���ɣ���ME��NF��ME=NF�ó��ı���EFMN��ƽ���ı��Σ�ƽ���ı��εĶԱ�ƽ�еó����ۣ���2���������ߣ��ӳ�EM��FN��AD�ڵ�G��H��֤����EMP�ס�MAG���������������εĶ�Ӧ�ߵı���ȣ��Լ����ε����ʼ�����⣻��3����PM��PN�ֱ�AD�ڵ�E��F�����ù��ɶ������EF����Ȼ��֤����PEF�ס�PMN���������������εĶ�Ӧ�߳ɱ���������⣮
�����������1�����Ȱ���Ҫ����ͼ����ͼ1��֤���߶���ȣ�ͨ��֤�����ڵ�������ȫ�ȣ�Ҫ֤��ME=NF����֤����MEP�ա�NPQ����֪�������������Ե�֤����ABP�ա�DCQ�����ı���ABCD�Ǿ��Σ����B=��C=90����AB=CD������BP=CQ����֪�������ABP�ա�DCQ��SAS�������APB=��DQG�����MPE=180�㩁2��APB=180�㩁2��DQC=��NQF�����MEP�ա�NPQ��AAS������ME=NF���ڡ�ME��NF����ֱ��BC����ME��NF���ߡ�MEP�ա�NPQ����ME=NF�����ı���EFMN��ƽ���ı��Σ�һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ�����MN��BC��
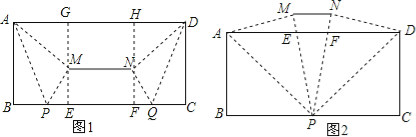 ��2���ӳ�EM��FN��AD�ڵ�G��H����AB=4��BP=3����AM=4��PM=3����AD��BC����EM��AD���ߡ�AMP=��MEP=��MGA�����EMP=��MAG�����EMP�ס�MAG����
��2���ӳ�EM��FN��AD�ڵ�G��H����AB=4��BP=3����AM=4��PM=3����AD��BC����EM��AD���ߡ�AMP=��MEP=��MGA�����EMP=��MAG�����EMP�ס�MAG����![]() ����AG=4a����EM=
����AG=4a����EM=![]() ��AG=3a,���ı���ABEG�Ǿ��Σ���BE=4a,��BP=3,��EP=4a-3,����EP=
��AG=3a,���ı���ABEG�Ǿ��Σ���BE=4a,��BP=3,��EP=4a-3,����EP=![]() MG=
MG=![]() ��4-ME��=
��4-ME��=![]() (4-3a)=3-
(4-3a)=3-![]() a����3-
a����3-![]() a=4a-3����ã�a=
a=4a-3����ã�a=![]() ����AG=
����AG=![]() ,ͬ��DH=
,ͬ��DH=![]() ����MN=GH=12-
����MN=GH=12-![]() ��2=
��2=![]() ����3����PM��PN�ֱ�AD�ڵ�E��F����AD��BC���۵�����ȣ����EPA=��APB=��PAE����EA=EP����EA=EP=x����EM=6-x,AM=AB=4����Rt��AME�У�42+��6��x��2=x2����ã�x=
����3����PM��PN�ֱ�AD�ڵ�E��F����AD��BC���۵�����ȣ����EPA=��APB=��PAE����EA=EP����EA=EP=x����EM=6-x,AM=AB=4����Rt��AME�У�42+��6��x��2=x2����ã�x=![]() ����EA=EP=DF=
����EA=EP=DF=![]() ,��EF=12��2��
,��EF=12��2��![]() =
=![]() ����EF��MN(��֤�������PEF�ס�PMN����
����EF��MN(��֤�������PEF�ס�PMN����![]() ����
����![]() ����ã�MN=
����ã�MN=![]() ��
��

����Ŀ��ȫ�����˶��ѳ�Ϊһ��ʱ�У�Ϊ���˽����о������˶��������ij�����ݵĹ�����Ա��չ��һ���ʾ����飬�ʾ����������Ŀ��A���������˶���B�����㳡����C���μӱ����ţ�D��ɢ����E�����˶���
�����Ǹ��ݵ��������Ƶ�ͳ��ͼ����һ���֣�
�˶���ʽ | A | B | C | D | E |
���� | 12 | 30 | m | 54 | 9 |
�������������Ϣ���ش��������⣺
��1�������ʾ�����Ĺ����� ���ˣ�ͼ���е�m=�� ����n=�� ����
��2��ͳ��ͼ�У�A������Ӧ������Բ�ĽǵĶ���Ϊ�� ����
��3�����ݵ�����������������ϲ�����˶���ʽ���� �������˶���������ռ�İٷֱ����� ����
��4�����б�ɳ�ڹ��Ǹ�������ϲ�����˶�����֮һ��ÿ������������������������ڽ���ij����Լ��1500�ˣ���ô����һ�¸������μӱ�ɳ�������������Ĵ�Լ�ж����ˣ�