Question

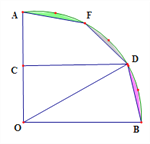
【题目】如图，扇形纸片AOB中,已知∠AOB=90,OA=6，取OA的中点C，过点C作DC⊥OA交于点D，点F是上一点.若将扇形BOD沿OD翻折，点B恰好与点F重合，用剪刀沿着线段BD、DF、FA依次剪下，则剩下的纸片（阴影部分）面积是______________.

Answer 1

【答案】；

【解析】分析：先求出∠ODC=∠BOD=30°，作DE⊥OB可得DE=OD=3，先根据S弓形BD=S扇形BOD-S△BOD求得弓形的面积，再利用折叠的性质求得所有阴影部分面积．

详解：如图，

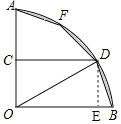
∵CD⊥OA，

∴∠DCO=∠AOB=90°，

∵OA=OD=OB=6，OC=OA=OD，

∴∠ODC=∠BOD=30°，

作DE⊥OB于点E，则DE=OD=3，

∴S弓形BD=S扇形BOD-S△BOD=×6×3=3π-9，

则剪下的纸片面积之和为3×（3π-9）=9π-27.

故答案为：9π-27．