题目内容
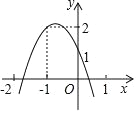
【题目】已知一次函数y=ax+b过一,二,四象限,且过(6,0),则关于二次函数y=ax2+bx+1的以下说法:①图象与x轴有两个交点;②a<0,b>0;③当x=3时函数有最小值;④若存在一个实数m,当x≤m时,y随x的增大而增大,则m≤3.其中正确的是( )
A. ①②B. ①②③C. ①②④D. ②③④
【答案】C
【解析】
根据题意可以判断a、b的正负,从而可以判断各个小题中的结论是否成立,从而可以解答本题.
解:∵一次函数y=ax+b过一,二,四象限,且过(6,0),
∴a<0,b>0,0=6a+b,故②正确,
∴b=-6a,
∴y=ax2+bx+1中a<0,b>0,
∴△=b2-4a×1=36a2-4a=4a(9a-1)>0,
∴图象与x轴有两个交点,故①正确,
在y=ax2+bx+1中,当x=-![]() =-
=-![]() =3时,取得最大值,故③错误,
=3时,取得最大值,故③错误,
∴当x>3时,y随x的增大而减小,当x<3时,y随x的增大而增大,
∴若存在一个实数m,当x≤m时,y随x的增大而增大,则m≤3,故④正确,
故选:C.

练习册系列答案
相关题目