题目内容
⊙O的半径OA=2,弦AB、AC的长分别为一元二次方程x2-(2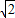 +2
+2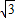 )x+4
)x+4 =0的两个根,则∠BAC的度数为 .
=0的两个根,则∠BAC的度数为 .
【答案】分析:先解一元二次方程,得AB、AC的长;再根据题中所给的条件,在直角三角形中解题.
解答: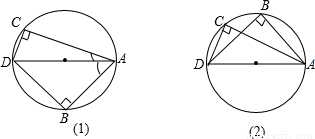 解:x2-(2
解:x2-(2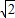 +2
+2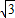 )x+4
)x+4 =0
=0
方程可化为:(x-2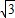 )(x-2
)(x-2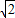 )=0
)=0
解得:x1=2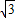 ,x2=2
,x2=2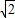 .
.
如图:(1)∵AC=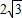 ,AD=4,
,AD=4,
∴cos∠CAD=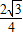 =
= ,
,
∴∠CAD=30°.
∵AB=2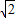 ,AD=4,
,AD=4,
∴cos∠BAD=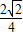 =
=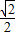 ,
,
∴∠BAD=45°.
则∠BAC=30°+45°=75°;
如图(2)
∠BAC=45°-30°=15°.
点评:本题考查了一元二次方程的解法和圆、三角函数等相关问题,着重考查了基础知识的综合应用能力,是一道很好的题目.
解答:
 解:x2-(2
解:x2-(2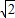 +2
+2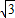 )x+4
)x+4 =0
=0方程可化为:(x-2
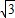 )(x-2
)(x-2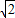 )=0
)=0解得:x1=2
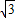 ,x2=2
,x2=2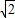 .
.如图:(1)∵AC=
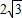 ,AD=4,
,AD=4,∴cos∠CAD=
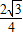 =
= ,
,∴∠CAD=30°.
∵AB=2
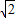 ,AD=4,
,AD=4,∴cos∠BAD=
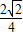 =
=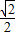 ,
,∴∠BAD=45°.
则∠BAC=30°+45°=75°;
如图(2)
∠BAC=45°-30°=15°.
点评:本题考查了一元二次方程的解法和圆、三角函数等相关问题,着重考查了基础知识的综合应用能力,是一道很好的题目.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
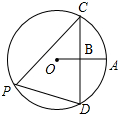 如图,点B是⊙O的半径OA的中点,且CD⊥OA于B,则tan∠CPD的值为( )
如图,点B是⊙O的半径OA的中点,且CD⊥OA于B,则tan∠CPD的值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
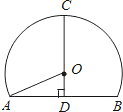 高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=10米,净高CD=7米,则此圆的半径OA=( )
高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=10米,净高CD=7米,则此圆的半径OA=( )
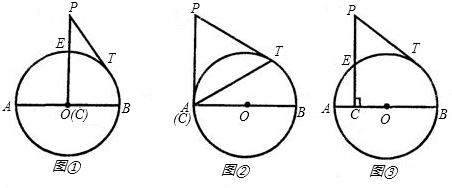
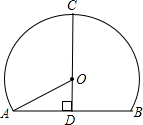 如图,是一个某一高速公路单心圆曲隧道的截面,若路面AB宽为12米,净高CD为8米,则此隧道单心圆的半径OA是
如图,是一个某一高速公路单心圆曲隧道的截面,若路面AB宽为12米,净高CD为8米,则此隧道单心圆的半径OA是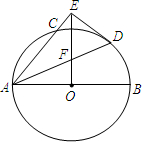 如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.