题目内容
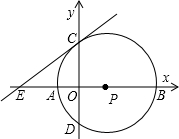
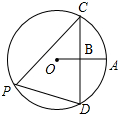 如图,点B是⊙O的半径OA的中点,且CD⊥OA于B,则tan∠CPD的值为( )
如图,点B是⊙O的半径OA的中点,且CD⊥OA于B,则tan∠CPD的值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:解答此题,需要将∠CPD转化到直角三角形中进行求解;连接OC、OD,由垂径定理和圆周角定理可得∠COB=∠CPD=
∠COD,因此只需在Rt△OBC中求出∠COB的正弦值即可.
| 1 |
| 2 |
解答: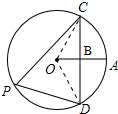 解:连接OC、OD;
解:连接OC、OD;
则∠COB=∠CPD=
∠COD;
Rt△OBC中,OC=2OB,则BC=
=
OB;
故tan∠CPD=tan∠COB=
;
故选D.
 解:连接OC、OD;
解:连接OC、OD;则∠COB=∠CPD=
| 1 |
| 2 |
Rt△OBC中,OC=2OB,则BC=
| OC2-OB2 |
| 3 |
故tan∠CPD=tan∠COB=
| 3 |
故选D.
点评:此题主要考查了圆周角定理、垂径定理以及勾股定理的综合应用.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
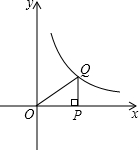 如图,点P是x轴正半轴上的一动点,过点P作x轴的垂线,交双曲线y=
如图,点P是x轴正半轴上的一动点,过点P作x轴的垂线,交双曲线y=| 1 |
| x |
| A、逐渐增大 | B、逐渐减小 |
| C、保持不变 | D、无法确定 |
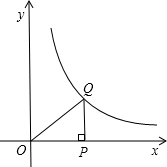 如图,点P是x轴正半轴上一点,过点P作x轴的垂线交函数y=
如图,点P是x轴正半轴上一点,过点P作x轴的垂线交函数y=| 2 |
| x |
| A、逐渐增大 | B、逐渐变小 |
| C、不变 | D、无法判断 |
 四边形OEDC是矩形,且OE=2OC.设OE=t(t>0),矩形OEDC与△AOB重合部分的面积为S.
四边形OEDC是矩形,且OE=2OC.设OE=t(t>0),矩形OEDC与△AOB重合部分的面积为S.
 (2005•遵义)如图,点P在x正半轴上,以P为圆心的⊙P与x轴交于A、B两点,与y轴交于C、D两点,⊙P的半径是4,CD=
(2005•遵义)如图,点P在x正半轴上,以P为圆心的⊙P与x轴交于A、B两点,与y轴交于C、D两点,⊙P的半径是4,CD=