题目内容
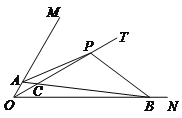
【题目】如图,已知射线OB平分∠AOC,∠AOC的余角比∠BOC小42°.
(1)求∠AOB的度数:
(2)过点O作射线OD,使得∠AOC=4∠AOD,请你求出∠COD的度数
(3)在(2)的条件下,画∠AOD的角平分线OE,则∠BOE= .

【答案】(1)44°;(2)66°或110°;(3)33°或55°
【解析】
(1)设∠BOC=x,则∠AOC=2x,根据∠AOC的余角比∠BOC小42°列方程求解即可;
(2)分两种情况:①当射线OD在∠AOC内部,②当射线OD在∠AOC外部,分别求出∠COD的度数即可;
(3)根据(2)的结论以及角平分线的定义解答即可.
解:(1)由射线OB平分∠AOC可得∠AOC =2∠BOC,∠AOB=∠BOC,
设∠BOC=x,则∠AOC=2x,
依题意列方程90°﹣2x=x﹣42°,
解得:x=44°,
即∠AOB=44°.
(2)由(1)得,∠AOC=88°,
①当射线OD在∠AOC内部时,如图,
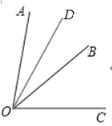
∵∠AOC=4∠AOD,∴∠AOD=22°,
∴∠COD=∠AOC﹣∠AOD=66°;
②当射线OD在∠AOC外部时,如图,
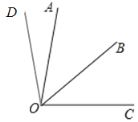
由①可知∠AOD=22°,
则∠COD=∠AOC+∠AOD=110°;
故∠COD的度数为66°或110°;
(3)∵OE平分∠AOD,∴∠AOE=![]() ,
,
当射线OD在∠AOC内部时,如图,
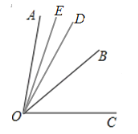
∴∠BOE=∠AOB﹣∠AOE=44°﹣11°=33°;
当射线OD在∠AOC外部时,如图,
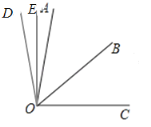
∴∠BOE=∠AOB+∠AOE=44°+11°=55°.
综上所述,∠BOE度数为33°或55°.
故答案为:33°或55°

练习册系列答案
相关题目