题目内容
【题目】如图，点D为△ABC边BC的延长线上一点．∠ABC的角平分线与∠ACD的角平分线交于点M，将△MBC以直线BC为对称轴翻折得到△NBC，∠NBC的角平分线与∠NCB的角平分线交于点Q，若∠A=48°，则∠BQC的度数为（ ）
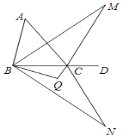
A. 138° B. 114° C. 102° D. 100°
【答案】C
【解析】
设∠ABC＝a°，根据外角定理可知，∠ACD＝∠A＋∠ABC＝48°＋a°，∵CM平分∠ACD，∴∠ACM＝
∠ACD＝24°＋
°，而根据三角形内角和等于180°可知，∠ACB＝180°－∠A－∠ABC＝132°－a°，故∠BCM＝∠ACB＋∠ACM＝156°－°，∵△MBC以直线BC为对称轴翻折得到△NBC，BM平分∠ABC，∴∠BCM＝∠BCN＝156°－°，∠CBN＝∠CBM＝∠ABC＝°，∵∠NBC的角平分线与∠NCB的角平分线交于点Q，∴∠QBC＝∠NBC＝
°，∠QCB＝∠NCB＝78°－°，故根据根据三角形内角和等于180°，∠BQC＝180°－∠QCB－∠QBC，未知数抵消，求出∠BQC的值.
设∠ABC＝a°，根据外角定理可知，∠ACD＝∠A＋∠ABC＝48°＋a°，∵CM平分∠ACD，∴∠ACM＝∠ACD＝24°＋°，而根据三角形内角和等于180°可知，∠ACB＝180°－∠A－∠ABC＝132°－a°，故∠BCM＝∠ACB＋∠ACM＝156°－°，∵△MBC以直线BC为对称轴翻折得到△NBC，BM平分∠ABC，∴∠BCM＝∠BCN＝156°－°，∠CBN＝∠CBM＝∠ABC＝°，∵∠NBC的角平分线与∠NCB的角平分线交于点Q，∴∠QBC＝∠NBC＝°，∠QCB＝∠NCB＝78°－°，故根据根据三角形内角和等于180°，∠BQC＝180°－∠QCB－∠QBC＝180°－78°＋°－°＝102°，故答案选C.
