题目内容
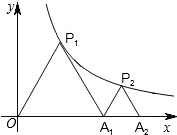 (2013•济宁三模)如图,P1是反比例函数y=
(2013•济宁三模)如图,P1是反比例函数y=| k |
| x |
分析:由于△P1OA1为等边三角形,作P1C⊥OA1,垂足为C,由等边三角形的性质及勾股定理可求出点P1的坐标,根据点P1是反比例函数y=
图象上的一点,利用待定系数法求出此反比例函数的解析式;作P2D⊥A1A2,垂足为D.设A1D=a,由于△P2A1A2为等边三角形,由等边三角形的性质及勾股定理,可用含a的代数式分别表示点P2的横、纵坐标,再代入反比例函数的解析式中,求出a的值,进而得出A2点的坐标.
| k |
| x |
解答:解:(1)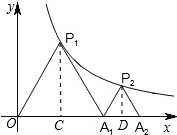 因为△P1OA1为边长是2的等边三角形,
因为△P1OA1为边长是2的等边三角形,
所以OC=1,P1C=2×
=
,
所以P1(1,
).
代入y=
,得k=
,
所以反比例函数的解析式为y=
.
作P2D⊥A1A2,垂足为D.
设A1D=a,
则OD=2+a,P2D=
a,
所以P2(2+a,
a).
∵P2(2+a,
a)在反比例函数的图象上,
∴代入y=
,得(2+a)•
a=
,
化简得a2+2a-1=0
解得:a=-1±
.
∵a>0,
∴a=-1+
.∴A1A2=-2+2
,
∴OA2=OA1+A1A2=2
,
所以点A2的坐标为(2
,0).
故选C.
 因为△P1OA1为边长是2的等边三角形,
因为△P1OA1为边长是2的等边三角形,所以OC=1,P1C=2×
| ||
| 2 |
| 3 |
所以P1(1,
| 3 |
代入y=
| k |
| x |
| 3 |
所以反比例函数的解析式为y=
| ||
| x |
作P2D⊥A1A2,垂足为D.
设A1D=a,
则OD=2+a,P2D=
| 3 |
所以P2(2+a,
| 3 |
∵P2(2+a,
| 3 |
∴代入y=
| ||
| x |
| 3 |
| 3 |
化简得a2+2a-1=0
解得:a=-1±
| 2 |
∵a>0,
∴a=-1+
| 2 |
| 2 |
∴OA2=OA1+A1A2=2
| 2 |
所以点A2的坐标为(2
| 2 |
故选C.
点评:此题综合考查了反比例函数的性质,利用待定系数法求函数的解析式,正三角形的性质等多个知识点.此题难度稍大,综合性比较强,注意对各个知识点的灵活应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013•济宁三模)如图,已知直线y=kx-6与抛物线y=ax2+bx+c相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上.
(2013•济宁三模)如图,已知直线y=kx-6与抛物线y=ax2+bx+c相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上.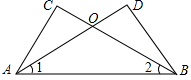 (2013•济宁三模)(1)一个人由山底爬到山顶,需先爬45°的山坡200m,再爬30°的山坡300m,求山的高度(结果可保留根号).
(2013•济宁三模)(1)一个人由山底爬到山顶,需先爬45°的山坡200m,再爬30°的山坡300m,求山的高度(结果可保留根号).