题目内容
 (2013•济宁三模)(1)一个人由山底爬到山顶,需先爬45°的山坡200m,再爬30°的山坡300m,求山的高度(结果可保留根号).
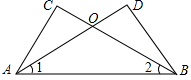
(2013•济宁三模)(1)一个人由山底爬到山顶,需先爬45°的山坡200m,再爬30°的山坡300m,求山的高度(结果可保留根号).(2)如图,△ABC与△ABD中,AD与BC相交于O点,∠1=∠2,请你添加一个条件(不再添加其它线段,不再标注或使用其他字母),使AC=BD,并给出证明.
你添加的条件是:
AD=BC;OC=OD;∠C=∠D;∠CAO=∠DBC等
AD=BC;OC=OD;∠C=∠D;∠CAO=∠DBC等
.证明:
分析:(1)由已知可得到山的高度由两部分组成分别是45°和30°所对的高度,所以利用三角函数分别求得这两部分的值,此时山的高度就不难求了;
(2)要使AC=BD,可以证明△ABC≌△BAD,从而得到结论.
(2)要使AC=BD,可以证明△ABC≌△BAD,从而得到结论.
解答: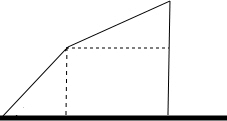 (1)解:依题意,可得山高h=200sin45°+300sin30°
(1)解:依题意,可得山高h=200sin45°+300sin30°
=200×
+300×
=100
+150(m)
所以山高为(100
+150)m.
(2)解:添加条件例举:AD=BC;OC=OD;∠C=∠D;∠CAO=∠DBC等.
证明例举(以添加条件AD=BC为例):
∵在△ABC与△BAD中,
,
∴△ABC≌△BAD(SAS).
∴AC=BD.
 (1)解:依题意,可得山高h=200sin45°+300sin30°
(1)解:依题意,可得山高h=200sin45°+300sin30°=200×
| ||
| 2 |
| 1 |
| 2 |
=100
| 2 |
所以山高为(100
| 2 |
(2)解:添加条件例举:AD=BC;OC=OD;∠C=∠D;∠CAO=∠DBC等.
证明例举(以添加条件AD=BC为例):
∵在△ABC与△BAD中,
|
∴△ABC≌△BAD(SAS).
∴AC=BD.
点评:(1)考查了坡度坡角的理解及解直角三角形的综合运用.
(2)考查了全等三角形的判定及性质;判定两个三角形全等的方法有:SSS,SAS,ASA,AAS,本题已知一边一角,所以可以寻找夹这个角的另外一边或者是另外两个角.
(2)考查了全等三角形的判定及性质;判定两个三角形全等的方法有:SSS,SAS,ASA,AAS,本题已知一边一角,所以可以寻找夹这个角的另外一边或者是另外两个角.

练习册系列答案
相关题目
 (2013•济宁三模)如图,已知直线y=kx-6与抛物线y=ax2+bx+c相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上.
(2013•济宁三模)如图,已知直线y=kx-6与抛物线y=ax2+bx+c相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上.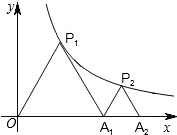 (2013•济宁三模)如图,P1是反比例函数y=
(2013•济宁三模)如图,P1是反比例函数y=