题目内容
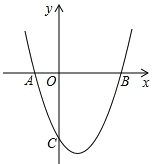
【题目】如图,抛物线![]() 的对称轴为直线x=
的对称轴为直线x=![]() ,与
,与![]() 轴交于A,B两点,与y轴交于点C(0,4).(1)求抛物线的解析式,结合图象直接写出当0≤x≤4时y的取值范围;(2)已知点D(m,m+1)在第一象限的抛物线上,点D关于直线BC的对称点为点E,求点E的坐标.
轴交于A,B两点,与y轴交于点C(0,4).(1)求抛物线的解析式,结合图象直接写出当0≤x≤4时y的取值范围;(2)已知点D(m,m+1)在第一象限的抛物线上,点D关于直线BC的对称点为点E,求点E的坐标.
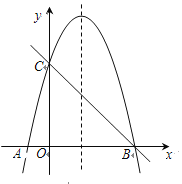
【答案】(1)、y=-![]() +3x+4;0≤y≤
+3x+4;0≤y≤![]() ;(2)、E(0,1)
;(2)、E(0,1)
【解析】
试题分析:(1)、首先将点C的坐标代入求出a的值,然后根据函数的对称轴求出b的值,从而得出抛物线的解析式,根据函数的性质求出y的取值范围;(2)、首先将点D的坐标代入解析式求出点D的坐标,然后根据轴对称性求出点E的坐标.
试题解析:(1)、将C(0,4)代入![]() 中得a=-1
中得a=-1
又∵对称轴为直线x=![]() ,∴
,∴![]() ,得b=3. 抛物线的解析式为
,得b=3. 抛物线的解析式为![]() .
.
当0≤x≤4时y的取值范围是0≤y≤![]() .
.
(2)、∵点D(m,m+1)在抛物线上,∴m+1=![]() .
.
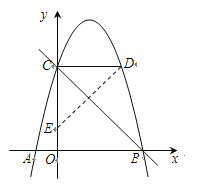
∴m=-1或m=3. ∵点D在第一象限,∴点D的坐标为(3,4)
又∵C(0,4),所以CD∥AB,且CD=3. 由![]() 得B(4,0)
得B(4,0)
∴∠OCB=∠DCB=45°. ∴点E在![]() 轴上,且CE=CD=3,∴OE=1. 即点E的坐标为(0,1).
轴上,且CE=CD=3,∴OE=1. 即点E的坐标为(0,1).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目