题目内容
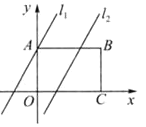
【题目】如图,在矩形ABCD中,点O为坐标原点,点B的坐标为(4,3),点A,C在坐标轴上,点P在BC边上,直线ι1:y=2x+3,直线ι2:y=2x-3
(1)求直线l1与x轴的交点坐标T,直线ι2与AB的交点坐标Q和与x轴的交点坐标G;
(2)判定四边形ATGQ的形状并求它的面积;
(3)已知点M在第一象限,且是直线l2上的点,若ΔAPM是等腰直角三角形,求点M坐标
【答案】(1)T的坐标为(![]() ,0),Q的坐标为(3,3),G的坐标为(
,0),Q的坐标为(3,3),G的坐标为(![]() ,0);(2)四边形ATGQ是平行四边形,面积为9;(3)点M的坐标为
,0);(2)四边形ATGQ是平行四边形,面积为9;(3)点M的坐标为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)根据坐标轴上的点的坐标特点可求直线l1与x轴的交点坐标T,直线l2与x轴的交点坐标G,根据直线AB上点的纵坐标特征可求直线l2与AB的交点坐标Q;
(2)从四边形ATGQ的两组对边的位置关系和一组邻边的数量关系进行判断即可;
(3)作图分三种情况讨论,设点![]() 的坐标为
的坐标为![]() ,根据证明三角形全等得到对应边长的关系,结合题目数据列出等式,求解x的值即可.
,根据证明三角形全等得到对应边长的关系,结合题目数据列出等式,求解x的值即可.
解:(1)直线l1:当y=0时,2x+3=0,解得![]() ,则直线l1与x轴的交点T的坐标为(
,则直线l1与x轴的交点T的坐标为(![]() ,0);直线l2:当y=3时,2x-3=3,解得x=3,则直线l2与AB的交点Q的坐标为(3,3),当y=0时,2x-3=0,解得
,0);直线l2:当y=3时,2x-3=3,解得x=3,则直线l2与AB的交点Q的坐标为(3,3),当y=0时,2x-3=0,解得![]() ,则直线l2与x轴的交点G的坐标为(
,则直线l2与x轴的交点G的坐标为(![]() ,0).
,0).
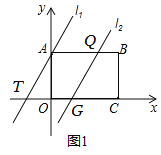
(2)如图1,因为直线l1与直线l2的k相同,都是2,所以AT∥QG,因为T(![]() ,0),G(
,0),G(![]() ,0),所以TG=3≠AT,又因为AB∥OC,所以四边形ATGQ是平行四边形,且平行四边形ATGQ 的面积=TG×OA=3×3=9.
,0),所以TG=3≠AT,又因为AB∥OC,所以四边形ATGQ是平行四边形,且平行四边形ATGQ 的面积=TG×OA=3×3=9.
(3)①若点A为直角顶点,点M在第一象限,AM=AP,如图2,过点P作PF⊥y轴于点F,过点M作MN⊥y轴于点N,则Rt△AMN≌Rt△PAF,∴MN=AF,AN=PF=4,∴M点的纵坐标为7,当y=7时,2x-3=7,解得x=5,即MN=5,∴AF=5,于是P点的坐标为(4,-2),∵点P在BC边上,∴此种情形点M不存在;

②若点P为直角顶点,点M在第一象限,如图3,过点M作MN⊥CB交CB的延长线于点N,
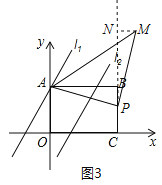
则Rt△ABP≌Rt△PNM,
∴AB=PN=4,MN=BP,
设M(x,2x-3),则MN=x-4,∴![]() ,解得
,解得![]() ,
,![]() ;
;
③若点M为直角顶点时,点M在第一象限,如图4,设![]() ,
,
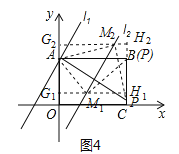
过点![]() 作
作![]() 交OA于点G1,交BC于点
交OA于点G1,交BC于点![]() ,
,
则Rt△AM1G1≌Rt△PM1H1,
∴![]() ,
,
∴![]() ,
,
解得x=2,∴![]() ;
;
设![]() ,同理可得
,同理可得![]() ,解得
,解得![]() ,∴
,∴![]() .
.
综上所述,点M的坐标为![]() 或
或![]() 或
或![]() .
.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案