Question

【题目】如图，在四边形ABCD中，AD∥BC，E是AB的中点，连接DE并延长交CB的延长线于点F，点G在边BC上，且∠GDF=∠ADF，下列结论错误的是（ ）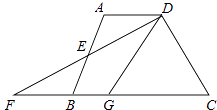
A.△ADE≌△BFE
B.AD+BG=DG
C.连接EG，EG∥DC
D.连接EG，EG⊥DF

Answer 1

【答案】C
【解析】解：∵E是AB的中点， ∴DE=FE，
∵AD∥BC，
∴∠A=∠ABF，∠1=∠F，
在△ADE和△BFE中
，
∴△ADE≌△BFE，所以A选项的结论正确；
∴AD=BF，
∵∠1=∠2，
而∠1=∠F，
∴∠F=∠2，
∴DG=FG，
∴AD+BG=BF+BG=FG，
∴AD+BG=DG，所以B选项的结论正确；
∵GD=GF，DE=FE，
∴GE⊥DF，所以D选项的结论正确；
而∠CDF不能确定为直角，
∴不能判断EG∥CD，所以C选项不正确．
故选C．