题目内容
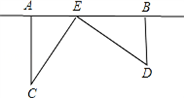
20、为了丰富少年儿童的业余生活，某社区要在如图所示AB所在的直线建一图书室，本社区有两所学校所在的位置在点C和点D处，CA⊥AB于A，DB⊥AB于B，已知AB=25km，CA=15km，DB=10km，试问：图书室E应该建在距点A多少km处，才能使它到两所学校的距离相等？分析：设AE=x，然后用x表示出BE的长，进而可在两个直角三角形中，由勾股定理表示出CE、DE的长，然后列方程求解．
解答：解：设AE=xkm，则BE=（25-x）km；
在Rt△ACE中，由勾股定理得：CE2=AE2+AC2=x2+152；
同理可得：DE2=（25-x）2+102；
若CE=DE，则x2+152=（25-x）2+102；
解得：x=10km；
即图书室E应该建在距A点10kmE处，才能使它到两所学校的距离相等．
在Rt△ACE中，由勾股定理得：CE2=AE2+AC2=x2+152；
同理可得：DE2=（25-x）2+102；
若CE=DE，则x2+152=（25-x）2+102；
解得：x=10km；
即图书室E应该建在距A点10kmE处，才能使它到两所学校的距离相等．
点评：此题主要考查的是勾股定理的应用．
练习册系列答案
名校课堂系列答案
相关题目
学校C和D的距离相等（C、D所在位置如图所示），CA⊥AB于A，DB⊥AB于B，已知AB=10km，CA=8km，DB=6km．
为了丰富少年儿童的业余生活，某社区要在如图所示AB所在的直线建一图书室，本社区有两所学校所在的位置在点C和点D处，CA⊥AB于A，DB⊥AB于B，已知AB=25km，CA=15km，DB=10km，试问：图书室E应该建在距点A多少km处，才能使它到两所学校的距离相等？
学校C和D的距离相等（C、D所在位置如图所示），CA⊥AB于A，DB⊥AB于B，已知AB=10km，CA=8km，DB=6km．