题目内容
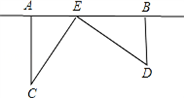
为了丰富少年儿童的业余生活，某社区要在如图所示AB所在的直线上建一图书室E，并使图书室E到本社区两所
学校C和D的距离相等（C、D所在位置如图所示），CA⊥AB于A，DB⊥AB于B，已知AB=10km，CA=8km，DB=6km．
（1）请用尺规在图中作出点E（不写作法，保留作图痕迹）；
（2）求图书室E与点A的距离．
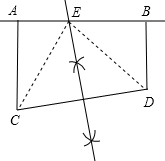
解：（1）
；
（2）连接CE、DE，
设AE=xkm，则BE=（10-x）km；
在Rt△ACE中，由勾股定理得：CE2=AE2+AC2=x2+82；
同理可得：DE2=（10-x）2+62；
若CE=DE，则x2+82=（10-x）2+62；
解得：x=3.6km；
答：图书室E与点A的距离为3.6km．
分析：（1）作出CD的垂直平分线，使之交AB于点E即可；
（2）作BF∥CD交所作的垂直平分线于点G，交AC于点F，利用勾股定理可得BF的长度，利用∠ABF的余弦值可得BE的长度，让10减去BE的长度可得AE的长度．
点评：考查线段垂直平分线的作图和有关解直角三角形的计算；作辅助线构造出直角三角形及平行四边形是解决本题的难点．
；
（2）连接CE、DE，
设AE=xkm，则BE=（10-x）km；
在Rt△ACE中，由勾股定理得：CE2=AE2+AC2=x2+82；
同理可得：DE2=（10-x）2+62；
若CE=DE，则x2+82=（10-x）2+62；
解得：x=3.6km；
答：图书室E与点A的距离为3.6km．
分析：（1）作出CD的垂直平分线，使之交AB于点E即可；
（2）作BF∥CD交所作的垂直平分线于点G，交AC于点F，利用勾股定理可得BF的长度，利用∠ABF的余弦值可得BE的长度，让10减去BE的长度可得AE的长度．
点评：考查线段垂直平分线的作图和有关解直角三角形的计算；作辅助线构造出直角三角形及平行四边形是解决本题的难点．
练习册系列答案
相关题目
20、为了丰富少年儿童的业余生活，某社区要在如图所示AB所在的直线建一图书室，本社区有两所学校所在的位置在点C和点D处，CA⊥AB于A，DB⊥AB于B，已知AB=25km，CA=15km，DB=10km，试问：图书室E应该建在距点A多少km处，才能使它到两所学校的距离相等？
学校C和D的距离相等（C、D所在位置如图所示），CA⊥AB于A，DB⊥AB于B，已知AB=10km，CA=8km，DB=6km．
为了丰富少年儿童的业余生活，某社区要在如图所示AB所在的直线建一图书室，本社区有两所学校所在的位置在点C和点D处，CA⊥AB于A，DB⊥AB于B，已知AB=25km，CA=15km，DB=10km，试问：图书室E应该建在距点A多少km处，才能使它到两所学校的距离相等？