题目内容
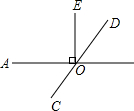
如图点O是直线AB上的一点，OC⊥OD，∠AOC-∠BOD=20°，则∠AOC=______度．
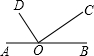
∵OC⊥OD，
∴∠COD=90°，
∵∠AOD+∠COD+∠COB=∠AOB=180°，
∴∠AOD+∠COB=90°，①
∵∠AOC-∠BOD=20°，
即∠AOD+∠COD-∠COD-∠BOC=20°，
∴∠AOD-∠BOC=20°，②
联立①、②求得，
∠AOD=55°，∠BOC=35°，
∴∠AOC=∠COD+∠AOD
=90°+55°=145°．
∴∠COD=90°，
∵∠AOD+∠COD+∠COB=∠AOB=180°，
∴∠AOD+∠COB=90°，①
∵∠AOC-∠BOD=20°，
即∠AOD+∠COD-∠COD-∠BOC=20°，
∴∠AOD-∠BOC=20°，②
联立①、②求得，
∠AOD=55°，∠BOC=35°，
∴∠AOC=∠COD+∠AOD
=90°+55°=145°．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
